「分数ものさし」小学生が発案 計算法、目盛りで理解：朝日新聞デジタル
苦手な子どもが多い分数の計算。それを視覚的に理解しようと、浜松市内の小学生＝当時＝が「分数ものさし」を考えた。長さ１２センチのものさしに５列の目盛りが付き、基準単位の「１２分の１」がいくつあるか数え…
記事によると
・苦手な子どもが多い分数の計算。それを視覚的に理解しようと、浜松市内の小学生が「分数ものさし」を考えた。
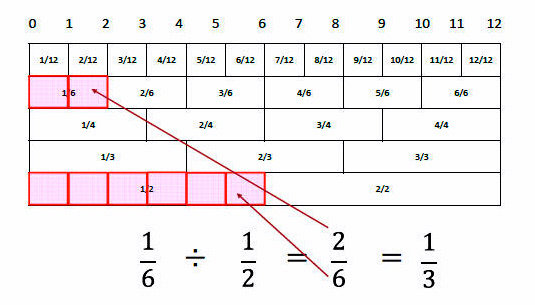
・長さ１２センチのものさしに５列の目盛りが付き、基準単位の「１２分の１」がいくつあるか数えて計算する。
・この発想に静岡大が注目し、教材化に向けた研究も進む。
・１とその数以外では割り切れない「素数」の目盛りだけがついた京都大の「素数ものさし」がヒントになった。
・苦手な子どもが多い分数の計算。それを視覚的に理解しようと、浜松市内の小学生が「分数ものさし」を考えた。
・長さ１２センチのものさしに５列の目盛りが付き、基準単位の「１２分の１」がいくつあるか数えて計算する。
・この発想に静岡大が注目し、教材化に向けた研究も進む。
・１とその数以外では割り切れない「素数」の目盛りだけがついた京都大の「素数ものさし」がヒントになった。
この話題への反応
・頭の中にこれがナチュラルに生まれない子が算数苦手なのかなあ
・コレ感動したわマジで！
・想定外に弱くなるのでは
・1/16は？とか考えちゃう当たりほんと自分は小物だと感じさせられる
・こりゃすばらしい。見える化されていて、分数嫌いの小学生たちに普及して欲しいね
・約分が理解できなかった、ということなのかね？
でも、その辺の話は学校で先生が黒板に書いて説明してくれないのか？
・なるほど分からん…と思ったが通分の概念を可視化するためのものかこれ、有用な子もいるかもね。私はインチの分数をこう表現したのが欲しい（´д｀）
・これはイメージしやすくて良いカモ！
・この図をみても、「割り算ではなぜ、割る方の分母と分子を入れ替えて逆数にするのか」わからなかったけど、分かる人には分かるんだろう。計三尺みたいで便利なんだろう。
・面白いねえ。計算尺ぽいな
1/8,1/12,1/24,1/36,1/48,1/72,1/144で作れそう
小学生で分数苦手な子多いからね
視覚的にわかりやすいと理解につながるのかも？
![GRANBLUE FANTASY The Animation 1(完全生産限定版) [Blu-ray]](https://images-fe.ssl-images-amazon.com/images/I/61rL4srJKyL._SL160_.jpg)
GRANBLUE FANTASY The Animation 1(完全生産限定版) [Blu-ray]
posted with amazlet at 17.04.03
アニプレックス (2017-04-26)
売り上げランキング: 2
売り上げランキング: 2
「ちゃうちゃうwww ワシ、チャウチャウちゃうでwwwww」
と
普通に計算した方が早くね
もともと分数の初歩ってこういう図を描いて教わるもんじゃないのか
かえってわかりにくいだろ
普通に勉強したほうがマシ
さっぱりわかんね
学習塾の教え方が悪いんじゃね
概念がはじめからわかってる人には意味は無さそう
わかる人間にとっては分からないってことが分からないからこういう道具が世に出るのはいいと思うぞ
何がきっかけで理解が進むか分からんしね
でも読んで真面目に勉強してろや
1／2で割るってことは2掛けることだからって頭の中で変換しちゃうから
こういう図はまったく出てこないな
それをさらに二分割してこれが1／4 etc
って普通の教え方だと思うんだがなあ…
誰か教えてくれ
例によって、これは俺には初見で何のこと言ってんのかわからんし
あくまで分数の仕組みを理解するためだけに使ったほうが良い気がする
基本は脳内暗算できるようにするようにしたほうがいい
可視化して頭の中で図を浮かぶ方が記憶として残りそうだから俺は逆に応用にも対応しうるとも思うが
ああ自己解決したわ
分数全部を12メモリに置きなおしてんのか
ここから計算に繋げようとすると余計に
わかりにくくないか？
そうそう。ただブロックに分割してるだけ
発案とかいってるせいで何か仕掛けがあるのかと思ったけど、ただの力技
ここがきっかけで計算の仕方に気付ける子もいると思うし
ない奴が計算苦手なんだろうな
分数理解してない人が見たら12cm固定である事でむしろ混乱をきたす
分度器の360度版にした様な円形を分割するものさしのほうがよっぽど分かりやすい
中学、高校とあがるにつれて数学は解きやすくなる
実物の方が視覚で理解しやすくなると思うのでこれは良いね
かけ算だから増える、割り算だから減るって概念ってどんな概念だよ馬鹿か
0.5掛けたら減るだろ。
0.5で割ったら増えるだろ。
に-1掛けたら大幅に減るだろ。
そんな俺的概念を植え付けると分数の割り算が出来ない子供になるんだよ。
加減乗商はなんでそうなるかじゃなくて基本原則だからって教えたほうがいい。
なんでそうなるのかは難しいから大きくなって勉強してね、でいいんだよ。
円周率も割り算なのになんで無理数になるのか殆どの人は理解していないだろ。
すまん植え付けない、だったなごめん
でも分数でつまずく理由って電気とかと同じで感覚的にわからないからだよね
とっかかりは重要だよ。こういう基本が理解できるようになったら早いからな
割られる数と割る数に同じ数をかけても同じだと言うことを理解すれば
分数同士の計算で分子分母に同じ数をかけて綺麗に整理するってのが簡単に分る。
これが分かりやすいって人は逆に凄い
手元に一覧表を置いてただろ。
これは初めて学ぶ子供が使うもんだ。
それにぐちぐち言うとか残念な連中だな。
その普通に計算するっていう所まで辿り着くのに使うんじゃないか？
何でググれば出てくんの？
三角関数を初めて学ぶ時に一覧表なんか手元に置いたら一生理解できない残念な子になりそう
まず単位円で定義を理解して、その後で簡単に計算できる30,45,60°を自分で計算するのがセオリーじゃないのか？
それ以外の角度はだいたい数値化する必要が無いし、数値化必須の場合関数電卓使用可だから一覧表とか出番ないだろ
なるほどね、最初の通分や約分の概念を理解できない奴に対しては有効かもな
頭の中でスムーズにやれてるから回りくどく感じるだろう
でも、分数が理解しにくいって人には確かにいい発明だ、これはわからない人にわかりやすいし説明しやすくなる
＞基準となる「１２分の１」が２個と６個と考えて、
＞「６分の２＝３分の１」と解く
なるほど！（わかってない）
常に持ち歩くんかいなって話に
まぁ普段生活してて計算する事とか皆無だがな
さすがに草
ケーキを切り分ける図解と何が違うんだ
逆に分数苦手になりそう
さっぱりわからん。(数学科卒)
あと何がわかるんだよこいつら
数字の意味も理解できてないというかする気も無いのか
他に理解できる事あるのか？
生きててつらくねーのか？意味はあるのか？
最初の「つまづき」をなくすのは大事。
上にある計算では視覚的に答えが１／３だと分かるし
小学生には単なる計算と割り切れずに理屈を知りたがる人もいる。
少なくともわいは視覚的に全く理解できんかった
これは素直に凄いと思う
成績ドンケツだったから同級生には理解されず、特に頭いい人。先生だけに利口と言われたっけ
視覚に囚われてかえって煩わしそうに感じる
なんなら、分母同士、分子同士を単純に割っても答えは出るんだぜ？
割り切れる場合だけどな
物差しとしての実用性皆無じゃねw
教科書でよっぽどシンプルに分かりやすく基本概念説明してるよ
頭のなかで考えてできるだろ
概念で理解しないと数学はできないぞ