
半分以上の人が解けないと話題の計算問題!「6÷2(1+2)=?」の正解がわかりますか?
http://matome.naver.jp/odai/2136248501140372101
台湾のfacebookコミュニティにて算数の簡単な式を出題したところ多くの人が間違った解答をしたという。
6÷2(1+2)=?
↑この問題の答え、わかりますか?
大勢の人が「1」と答えた
だが・・・
正しい答えは「9」となる。
中略
正解:
6÷2(1+2)=
6÷2(3)=
3(3)=
3×3=9
(全文はソースにて)
まさか同じメーカーの電卓で答えが違うとは思わなかった:(;゙゚'ω゚'): twitter.com/kouzukifukurou…
— フクロウ@卒業確定さん (@kouzukifukurou) 2013年3月5日>数学者数名に話を聞いたところ人によって解がことなり、そもそも問題の書き方がおかしいという指摘があった。
問題があんまり良くないな・・・
1かと思ったわ
これって文字式じゃないから2とかっこの間に×をいれることは出来ないと思うんだけど...... getnews.jp/archives/114382
— 暇ネコさん (@himaneko1) 2013年3月5日関連記事
【「7+7÷7+7×7-7」 ← この答えが分かる人は頭がいいらしい】
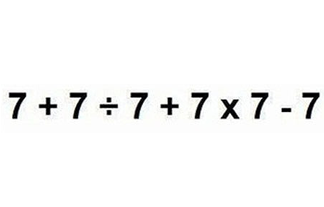

figma ひだまりスケッチ×ハニカム 宮子 (ノンスケール ABS&PVC塗装済み可動フィギュア)
Max Factory 2013-07-31
売り上げランキング : 1
Amazonで詳しく見る
TV ANIMATION BLACK ROCK SHOOTER ねんどろいど チャリオット with 戦車 (メアリー) セット TV ANIMATION Ver.
グッドスマイルカンパニー 2013-07-31
売り上げランキング : 3
Amazonで詳しく見る





7だと思っちゃった
罵ってくださぁい
間違ってたら小学校からやり直しだよw
二年位前に見たわー
じゃあこれがまずダメだろ
1になるじゃん
割り算が掛け算より優先され+-は後だと知っていれば馬鹿でもわかる。頭が良いかどうかじゃない。
出来なかったら中学生あたりからやりなおし
この流れがわからんw
6÷6=1じゃねぇーの?
後、別にこれを正解できたところでどうということはないw
出題者がバカ
でも9でもいいし
どちらにしろ式が不完全だよこれは
2(1+2)と2×(1+2)は別物だよ
括弧内の計算→除算・乗算→減算・加算
はさすがに一般常識でしょ
でもこれ小学生の頃に習ったような…
2xにはならないだろ?
×を省略したら2(1+2)で一つのかたまり
それだな
学校で習った計算方法の中で別のに変えると答えが変わってしまう問題だわ
これが数式の穴か
どうやったらそんな計算になるのか本気で分からないんだが…
だれか解説してくれ
6になったよ
つかこんなのも解けない半分の人って、どの半分なんだよ…
あったら、9。
3(1+2)=(3+6)
=9
3(3)=
2x3ってなってると思った
答えはソニーが悪い
()あるのに先に外計算するとか無いから
これが正解だな。
分数にしてみろって…
それとも6!!!!みたいに馬鹿にはわからん引っかけですか
1になる人は6÷2(3)のところで2×3をしちゃう
基本的に()内以外の掛け算割り算は左から解くから先に6÷2を先にしないと間違えるパティーン
もしかして年代で回答が割れたりすんのかなこれ。
どっちでもいい気がする
2(3)=6になって1だろ?
紛らわしい
こういう話題のやつはすぐ出来る。
そういう公式だけ記憶するタイプの人間のほうが将来応用が効かなくなるんじゃないかと
自分で感じてるんだけど。
6÷2(1+2) → 6÷(2+4) → 6÷6=1
=6÷2(3)
=6÷2×3 ←ここで×付けるとさすがにわかるだろ
=3×3
=9
俺たちの文明がここから崩れ去るとは誰も予想していなかった
記号や塊の表記は統一しないと、ただの意地悪問題だよ。
省略した場合はその数式を塊として捉えるって計算もあるから。
これで「どうやったら1になるかわからん。」って書いてる奴は馬鹿。
ちなみに自分、数学の成績は壊滅的でした^^
文系のクズだろ
文字式に置き換えないなら9
文字式に置き換えないなら9
6÷2(1+2)→ 6÷(2+4) → 6÷6=1 じゃないの?
x=(1+2)として6÷2xで計算しても良いと思うけど。
学生の範囲を指定しないと、答えもばらつくぞw
✕は省略されてるんじゃなくて多項式っつー概念なのよ
だから優先順位は四則演算よりも上
知識が無いから1になる
俺37だけど小学校で習ったやり方だと1になる。
しかし問題は 6÷2(1+2) なので1という答えも
が無いときはxの記号を省略できないって何回も
解けたから俺すげえお前ら馬鹿ってモンでもねーよ
おっさんよりゆとりのが解けるだろ
これを6÷2×(1+2)として考えるのは知識がなさ過ぎる
マジで
ていうか、どうやったら1になるのか理解不能
大多数は普通に9と答えると理解しろ
高校くらいなら複数正解になりそうだな。
コメントしている人はおそらく嘘を言っている人も半分以上いるな
間違えた人に「こんなの間違えないだろ」とか言って優越感に浸っているけど本当は自分も最初間違えた人だと思う
だから、その×を省略している前提が成立していないといわれているw
お前の知識がないだけ
*省略とか覚えてねえよ
ユニットで考えちまうわ
()の計算も出来んお前が小学生からやり直せ
あなたの両親は亡くなっていませんね
あなたの両親は亡くなって、いませんね
みたいなもんじゃないか
天才なら問題を見た瞬間出題者の意図を読み取ることができる
まあ世の中才能だわな
のうきんガリ勉がいくら勉強しようが丸暗記し出来ないということwwwwwwwwwwwwwwwwwwww
俺は自分で頭が悪いと思っていたが頭が良かったのか。
結局1でも9でも正解って言える問題。
小学生のドリルのやり方だと答えは9になるけどなw
6÷2(a+b)=?
お前馬鹿だろ。
記事に大勢の人が「1」と答えたって書いてあるのが読めないのか?
小学校の計算方法だと9
高校以上の計算方法だと1or9
小学生が9、それ以上は1でいいな
問題に問題があることを問題にすることが問題である
×省略してなかったら9
括弧がどうかかるか忘れてるヤツ多すぎ。
現役の学生なら絶対間違えないレベルだけど大人になると結局みんな忘れてる。
2*(1+2)だろうが2(1+2)だろうが答えは6だろ
問題は割るのが先か分配が先かだろ
ドリルなら×なんて省略しねーよw
6÷ 2(1+2) なら9 かな。
どこまでが分母になるか分かりにくい。記号統一してないし。
あんまいい問題じゃないな。
検索結果は問題がオカシイ、解なし、1とかなんだけど
1だと思ったらけど改めて見たら9でした。
半分以上の人が解けない計算問題なわけだが
足し算引き算は後
ただし()内は最優先という当たり前の規則を守っていれば
間違えようがないんだが
コメント欄でどちらが正解論争しててワロタw
しかしやっぱ同じ感想の人多いな
文字式無しの算数で乗算記号省略なんてしないよな?
なんで1になるのか分からないなら小学校からやり直した方が良い。
うちはやってたんだけど?w
数学の知識だと()優先するから1
そりゃ、不良品だなw
それに「省略した場合は四則演算に優先して計算する」って条件が入ったり入らなかったりするから
そもそも問題としてダメなんだよこれ。
ちなみにセンター200点ですわ
6÷2(1+2)=?
6÷(2*1+2*2)=?
6÷(2+4)=?
6÷6=?
1=?
間違いなのか?
今更じゃんかこんなの
人間にとって最も有害で脅威的なものは池沼だ
私には分かるのだ 下等民族がもたらした放射性物質、PM2.5、人工花粉が確実に私の体を蝕んでいると
1か9だった
>「記号を省略した場合、その部分を塊として計算する」
そんなものはありません。
そうしたら9になる
()を優先しても9ですけど?
これがokなら次式が成り立つわ
33 = 9
3(3) = 9
3×3 = 9
こう書いてくれたら誰も間違えないわけで表現が悪いとしか言いようがない
なぜ、2(1+2)を先に展開する?
官僚、政治家、企業幹部
屑に殺されるぞ
端的に言うと「いじわる」な問題
サイコパスと精神疾患者は9と答える
>おかしいという指摘があった
って記事に書いてあるにもかかわらずドヤ顔で人をバカにする奴はちょっと…
省略する場合は計算優先って解説もググったら普通に出てくるしな。
3は()についてるんじゃねえの?
俺もそう計算した そうすれば計算の順序が今までと一緒の形にもっていけるし
×を省略した部分は項として扱うから1だよ
もしくは数値式で×を省略してはいけないから解なしか
これで9が正しかったら6÷2aの答えが3aになる
文系はバカだから9と答える。
あと2(で間に×無いととか言ってるバカも小学生からやり直してこいww
()の中計算が先でその後は普通に左側からある÷、×の順で計算するって
算数で習っただろwwゆとりかww
正解見て同じで片方の意味わからんって言ってる奴のが頭おかしいわな
だから高卒なんだよ・・・
したがって解なしが正解
÷と掛け算の省略の併用はしてはいけない
お前ら日本語も読めないのかよ
そんなに解きたいなら1+1=2である証明でもしてろよ
割り算の記号はあるのに、掛け算の記号は省略している場合は?
という指摘は無視かw
小学校しか出てないと9が正しく見えるよね。
よって、9と答えた人は算数レベル。
の順だっけか
おれもそう習ったから9だけどこれって算数的に答えてる人と数学的に答えてる人で争ってる感じだなw
ニコニコ大百科のこの問題の記事見てみるといいよ。
結構面白い議論しているから。
数学が全然だめだったから9って思ったんだろ
理系大院卒だけど、9だな。1と言ってるお前はFランなんだろうな
うどん
だからこそこの問題があるわけで
分数に直すほうが頭やわらかい
頭悪かったけど今は頭いいアピールはいいから流れ読めよ
普通に9って出るけど。
まず問題の出し方おかしいって言ってんだから
これ間違えただけで
「お前らゆとりかw」とか
自分に酔うのやめたら?キモいよね(笑)
A(B+C)=AB+ACとなる
省略されてれば一つの文字扱いになることを失念している
(間違い)最終的に6
(訂正)最終的に1
屁理屈だがもしこういう式を取り扱う時が来たときどうする?
そんな時があるかどうかも知らんが
お前は一番の馬鹿だな、算数で考えても数学で考えてもおかしい計算すんな
これは一種の数学的ジョーク
真面目にどちらが正解か議論してるほうでおかしい
つまりこれは算数というわけなんだよな
あんま頭良くないし混乱するわ
でも()内は先に計算する
っていうのがルールじゃなかったっけ?
それ、文字式だろw
だったらA=1+2でいいよな ()の意味ないよそれ
括弧内がどうとかこれはそういう話ではない
2×3とは違うのか
乗を入れられないとするならそもそもこの問題自体が成り立たないんじゃないの?
数式としておかしいで終わりか?
6÷2×(1+2)の×を省略しても6÷2(1+2)にはなんねえよ。(6÷2)(1+2)だ。
逆に、6÷2(1+2)で×を省略せずにかくと、
6÷{2×(1+2)}=1
お前は数式とか見ないの?
どんだけ数学使わない学科なんだw
それに、いまどき理系で大学院卒は当たり前だろ。
置換を利用して(1+2)=a
とすると答えが1以外にはならない
数学的には問題に不備があるんだよ
除算乗算は左からだもんなぁ
結局、省略を優先するかしないか書いてない段階で問題がダメ。
左から計算だ厨と、省略箇所優先だ厨が永遠に戦ってる
問題自体が間違えているという結果だったな
9だと思う奴は例えば6÷1(1+2)=18だと思ってるの?
実際は6÷(1+2)=2なのに
括弧内が先じゃないのか?
6÷2+4 =
3+4 =7
こうはならないの?
ワロタwww
つまり教科書が悪い
なるほど、そういう事か。
じゃあ9で決まりだ。
ありがとう、すっきりした。
指差して笑われるようじゃなきゃ
どっちでもいいや
それだけはない
2(1+2)は先に計算しちゃダメなの
あくまで先の6÷2が優先なんだよ
(1+2)をaと置くと、6÷2aで
6/2aで1になるんだよなぁ
多分1って出た奴はプログラマーが多いだろ
新しすぎる
6÷2(1+2)=6÷2+4
=3+4
=7
どっちかの答えにどうすればなるのかわからない奴はただの馬鹿
どや顔で()内が先で×は省略されるとか言ってる奴は問題はそこじゃないことに気づいていないからもっと馬鹿
優先順位はある。逆にないと分母の数値が違って、答えがはちゃめちゃになる
あとは掛け算と割り算が左から順に優先度が下がる。
こんな感じだった気がするな
どっちを正解としてるかわかるぞ
プログラムで書くと9になるかと
俺自身はプログラムに関してたいした知識持ってないから間違ってるかもしれんが
一か八かにしよう
僕は答え1にしました
そもそもの問題が普通に使用するものとしたらぶっ壊れてる。おしまい。
と思って答えたら当たり でも式おかしいね
どうしたら答えが~~になるんだよ、って言ってる奴は問題が解けても馬鹿
馬鹿は答えに悩まない
それ意味ないだろ
9派はそれを(6÷2)(1+a)として計算するんだから
これを2×(1+2)と考えるのははっきりと間違ってるぞ
これは2(1+2)で一纏め
乗算記号を省略していると考えるなら省略した部分を先に計算しないといけない
数値式だから乗算記号の省略なんかありえんと考えるなら問題が誤り
と書けばほとんどの人が9と答えるだろうから、これは問題の表記の仕方が悪いとしか言えん
これは数学じゃなくて算数だよね
中学生以上の数学で考えれば1になるわな
算数で掛け算の記号を省略していいなんて習わないけど
確実に言える事はテストや試験でこの問題は出せないと言うことだな
イチゴ+ミカン+バナナ+マグロ=?
答え・ミックスジュース
おっさんのみんな頭悪すぎや…
文字式と考えないなら×を省略してはいけないから問題に誤りがあるで終わりだよ
プログラムを書くときはどっちで計算させたいかを考えてカッコを付け足したりするから、プログラマーがこの問題を見てどっちに解釈したかによるかな。
プログラマーなら、たぶん1になるように書くけど。
算数ならなおさら2(1+2)の部分がおかしくなるんだがな
2(1+2)は先に計算しちゃダメなんだってば!
左からなんだってばよ
そもそも文字を使わない状態で省略なんて普通しないんだよ
省略された状態はブロックで考えることが普通になっているから
問題を手直しせざるおえない
9派は 9=6÷2×(1+2)
1派は 1=6÷2a a=(1+2)
で計算してる
数学と算数でルールが違ったら大事だろ
答えは出題者の意図によるでいいだろ
完全に問題の作成者側のミス
試験だったら両方正解にして訂正するレベル
6÷2(1+2)=
6÷2(3)=
3+(3)=
3+3=6だと思ってしまったあああああああ
+なんてどこにもないのに・・・
こんなことに引っかかってしまった自分が情けない
そうなると
6÷2(1+2)
3(1+2)
3+6=9
答えはあってるけど式が違う
これ小学生で習う算数じゃねーかよ。
これが解けないとかどんだけゆとりなんだよ。
6÷2AとA=(1+2)で答えどうなんのよ
6÷6=1
って計算すると1になる
6÷(2(1+2))=
9であってるかもしれないけど1の解き方を考えられないのはどうやって学生時代を乗り切ったのか疑問
え?「ゲロマズ」かと思った
文字式の概念無いから掛けるが省略されてる前提で動くんだろ
33=9とかになるだろがw
と思ったらやっぱり変なのね
()の右はかっこの係数ってのがお約束なのでは
数学的に9ってどうなの?
で、2×(1+2)と2(1+2)を同じものだと思ってる奴は因数分解をもう一度勉強しなおした方がいい
6÷2(1+2)=6÷2×(1+2)とする考え方は存在しない
算数にも数学にもこんな計算の仕方は存在してない
2と(1+2)の間に×記号が省略されていると考えるなら
6
ーーーーー
2×(1+2)
と考えるものだよ
普通に÷の後に掛けりゃいいんじゃねえの
お前は数学の世界に3×3という表記が無いと思っているのか
1と9で迷ったやつが正解
迷わなかったやつは公文へGO!
2aとかなる時点でモヤるわ
学校じゃここを先に計算するよう習ったな
小学校からやり直せ
文系乙
これは因数分解の問題だよ。
6÷(2a+2b)=c
a=1, b=2なので
6÷6=c
c=1
掛け算は式から省略できるなんてルールしらん
9以外なんなんだ
ちなみに学力は下
文系理系関係ないような
最近言われているこの式が成立していないという計算方法ですると1
話にならん
俺も先に計算するって習った気がする
6÷2x(1+2)じゃないから
それはそれでお前も頭悪いと思うが…
6÷2(1+2) だったら日本語的には答えは3かなあ
6÷2=3, 1+2=3 すなわち 3(3)となって並列に書いてるだけっていう判断
これは1だと思うな
6÷2 が (1+2) にかかる
だから 3(1+2) になるんじゃね?
よって答えが9
日本終わってんな
6÷{2×(1+2)}なのか
で分かれるな
僕は悪くない。
いくつでしょう!?
6÷(1+2)=6÷1(1+2)
6÷1×(1+2)=18
なんてする馬鹿は居ないだろ?
答えは2だ
1っていってるのがゆとり以前世代、9っていうのがゆとり世代。
ゆとり以前世代で9って言ったりゆとりで1って言ってるのはただのアホ。
”どうみても~”とか言っちゃうのはたまたま正解だっただけで有頂天な
思考停止のゴミ屑。
算数的に答えれば9数学的に答えれば1なだけだろ
一番バカなのは1に決まってるとか片方しか考えられないやつな
本屋行って小中学生の問題集見て似たような問題解いて来い
1に決まってるだろ
最近は違うのかな
どちらにしても片方しかわからない言ってる人が一番あかんやろ
答えが9になるのは小学生の算数だ。
中高行ってたら普通1になるわ
小学生じゃなくて中高の数学やり直せアホか
ほんとに間違えてるやつが大勢居るとは。
括弧とそれに付随する数字で1つの固まりとなり、それを先に計算すると習うからね。
つまり、「2(1+2)」で1つの数字になるのでこの部分は「6」となり、「6÷6」で「1」になる。
もちろん、「2×(1+2)」という表記であれば、「2」と「(1+2)」は別の固まりになるので「6÷2×3」となり「9」になる。
単純に「数学」(算数にあらず)を教えられた時期にもよるかと思うけれどね。
ただ「算数」の問題として考えた場合、乗算記号を省略し、“勝手に”(←ここ大事)代用すると言うと言うルールは習う事はないので、それを勝手に行なっている人はルールを勝手に改変していると言われても仕方ないかと。
×の省略が成立するのって後にカッコがつく場合だけだからこういう場合って
省略された×もカッコの一部になるような気がしてたわ・・・特に教えられたわけでもないのに
あ、加減乗除は優先順位があるんだったっけ?
割り算と掛け算では割り算を最初にするとか習った気がするなw
6÷2x と 6÷2×x じゃ全然違う
どちらか片方だけが正解って言ってる奴が馬鹿だってことで
6÷2(1+2)
じゃなくて
6÷2×(1+2)
とすべき。
文字式だと2xとか2bのように、2(1+2)を先に計算してしまうから解答が1になってしまう。
単純に数字の計算だと括弧内を先に計算して、加減乗除の優先順位通りに計算するんで、6÷2×3を計算して解答は9になる。
掛け算の×を略した数字のみの式にした時点で出題者の失策、試験なら解答が1でも9でも正解になるパターン。
算数では~と言ってる人もいるが、算数では2(1+2)を計算出来ない
2(1+2)を2×(1+2)と考える場合は
6÷2(1+2)=6÷{2×(1+2)}と考える算法しか日本には存在しない
>>415みたいな曖昧な部分があるから、使わないし。
無理矢理引っかけようとひねり出した問題だからしょうがない
問題の本質がわかってないってことだからな
6÷2×(1+2)の×は省略しちゃいけない
2(1+2)と書いてあって、この部分を先に計算しては
いけないなんてルールは絶対ありえない。
>>427はいい指摘してる。
6÷{2(1+2)}なら1になるけど
問題のように
6÷2(1+2)なら9だよ
()>÷×左から>+-左からの優先順位と教わったが?
1組につきビスケット1枚・クッキー2枚のお菓子を配ります。
さてお菓子は全部で何枚必要でしょうか。
ゆとり「1枚!!!」
÷を使ってる以上これは算数
はい答え出ましたね
1と答えた皆さん 問題を良く読まないと
まだまだですね
2.×÷左から
×を省略していいのは文字式だけだから問題が不適。仮に×を省略しているとするなら
2(1+2)={2×(1+2)}になるから問題文は6÷{2×(1+2)}にしか読めないわけで
答えは1になる。
ただこの問題の作者はたぶん世代によって()を先に計算すべしと教えられたか÷を先に計算すべしと教えられたかによって答えが違ってくる日本の妙な教育を皮肉っているだけなんだろうけどな。
上に書いたみたいなような文字式の理解があればこんなことになるはずもない。
まぁここでそんな理解もなく9だ1だとバカさらしてるのが今の日本の教育レベルだということだ。
わかりやすい例えだな
出題者に6÷1(1+2)は?って言ってみたら面白いんだろうな
6÷2aを計算するときに6÷2×aと計算してはいけない
とも習わなかった?
その後左から解いたら9だ
数学じゃ普通にバラバラに計算してますが?
そもそも×を省略できるのは、2aとかの係数であって、
これは(2×a)って意味。
数学じゃその部分だけ先に計算しろって意味がある。
その記号を使ってる以上、正解は1。
×を使ったなら9.
割り算は記号略せないからね、分数形式にするしか略す方法無いよ。
6÷2a=3aになっちゃうだろw
×を省略した時点で、多項式となる。
9になるためには×を省略しちゃいけない。
間違えたら「ひとつ勉強になった」と思っておけよ
解答無しが正解
1とか9とか書いてるやつは何か勘違いしてるんじゃねーの?
数学者ですら答えが分かれるとなっては凡人にはどうしようもないな
その通りだね。
この出題者は6÷1(1+2)=18って答えるんだろうか?w
係数記号のルールも知らないバカ。w
算数では2(1+2)を計算できませんよ
6÷2×(1+2)だったら9が正解。
左から先に計算するってルールがある。
でも係数記号は、その塊だけ先に計算するってルールがあるから、
6÷2(1+2)と書いたら正解は1だよ。
明らかに出題者が間違ってる。
それ言ったら算数の範囲では×の省略は解けないよ
あれたしか数学の範囲でしょ
数学では/記号のみを使って÷記号を使ってはいけない
なんてルールは存在してませんが……
かけて欲しい場合は2・(1+2)と表記し
割って欲しい場合は[2(1+2)]と表記するんだけどね
だからそれだと×省略不可だって
算数じゃ「÷と×」のペアで
数学じゃ「/と ・」のペアで習うんだよ。
この二つがごっちゃになる問題なんて見たこと無い。
なんちゃって理数系君は読解が苦手みたいですね
分数に直したって1になるぞ
6÷2(1+2)は9
理由はそう習ったから
1が間違ってるってのが間違ってるのは確か
これを9と答える奴は真面目に数学やってないだろ
なんだこれって解いたら1になったけど、そもそも変なカタチしてて気持ち悪い
どーでもいいよこういうの
だーかーらー
6÷2aは6÷2×aという計算をしない
6÷2aは6÷(2×a)という計算をする
とも習ってるはずでしょ?
係数と見るしか無い
半分以上解けると思うけどね…
式を改変する頭のおかしい人は9
積と商、和と差の優先度はそれぞれいっしょだね
商>積というわけじゃない商=積
にならない理由は?
ちなみに俺のカシオの関数電卓でも答は1だった。
やっぱり3C学ばないような底辺文系は面白いなwww
2*1+2*2 =6だから
まてまてまて
お前の頭が悪いから
ルールはないから。w
2aって書いた時点で、2aを先に計算するのが数学のルール。
つまり問題は「1」が正解。
出題者はバカ。
(´・ω・`)
ついに幼稚園児まで現れたか…
そんなことしたら交換法則とか成り立たないやん!
2・3÷2・a=3aで
6÷2×(1+2)の表記なら間違える人はいないだろうけど
これだと6/{2(1+2)}という意味に見えかねない
それは×の省略を知らない小学生のためのルール。
省略をした時点で、その部分の掛け算は()の中の次に優先される
疲れてんのかな
どう考えても1だったわ
左からというのは全てにおいて基本となる法則
だからこそ交換法則が成り立つ
本来左からだが、交換法則により順番変えて計算できる
使えます
X÷2Yという表記は数学的になんの問題もない
xに正解の数字を入れるって感じの
検算方法とこれは同じじゃね?
どっかをxって考えたら
そうならない?
だからあってると思うのは俺だけ?
いや、結果は同じなんだけど()の数字とその前の数字は一組と考えるから通常優先順位は上
答えは1以外にありえないです
中学生からやり直せ
記憶違いか教える人がわかりやすいように説明したんだろう
和と差、積と商に優先順位はないよ
9って数字が出てくるような文を示してくれたら理解してやってもいいよ
だけど
2×3≠23
文字式じゃないのにこんな書き方はしない
問題が悪い
いやだからさ…
もういいやw
2(1+2)と考えて(2+4)で6として
6÷(2+4)で1となるかはまあ人によって違うだろうなぁ…
……、
この式の利用方法がわからない。
6÷2=(1+2)=9
なんで割ってんのに6より大きくなるんだ??
?
6÷2×(1+2)なら9で間違いないんだが
何を言ってるんだ…
9になる人の計算過程は
(6÷2)×(1+2)=3×3=9
→6÷(2+4)→6÷6=1
>>435
計算式の書き方が間違ってるんだから解釈の違いでいくらでもできる
まあそうね
誰かやってくれ
もしかして9とか言ってるのは半島出身の方々ですか^^;?
確かに大陸や半島の計算方法では9になるしソース元の台湾でも9が教科書的に
正しいってあったけど、ここ日本ですから・・・w
劣化させたの?
それとも1が正解なの?
過程を見せろ電卓!
>>520の煽りは流石に引いた
それ以前に>>435はなんか計算が全然違う気がするんだが・・・
(´・∀・`)
ポケップポポポポペッポッペー!!
お前さんはマイナスが出てくる時点で論外
正解は1ということで
一般人の答え→え?1じゃないの?
ネット民の答え→当然9だろjk
おれはまだ一般人だ
よかった
というか、
与えられたビスケット1枚・クッキー2枚を2人で分けるときに新たな問題が発生しそうな気がする
関係ないからどーでもいいけどw
数学者すら答えがわかれるのに9をボロクソに叩くのはどーなの
引っ掛け問題のつもりで出題者が勘違いしてないか
()の手前の×は省略可能 って意味じゃないぞ
商と積は同じ順位で左から順番に処理される
ただ積の省略が厳密に定義されてたかどうか
BNCとかで構文解析書いてても迷う事あるんだよね
答えは? → 問題がおかしい!
そりゃ1点にもならんよ
6÷2×(1+2)だと9になる
問題の×が係数になってるから紛らわしい
1とかマジで言ってんの?
3をカッコないの1+2それぞれにかけて、
3+6
やっても9だった。
でも関数電卓にそのままの式を入れると1に。
2とカッコの間に×入れると9になる。
x÷2x=0.5x^2 と答える人なら9
おれは前者だな。
ここで違うこと書いてる人もいるみたいだから、
迂闊に信じたらダメだと思うよ。
1になるときは係数扱いになってる
9になるときはxの省略だと扱ってる
9で何も引っかからない奴は
多分数学苦手だっただろ
6÷2×(1+2) って書けよ
2(1+2)だと係数の計算になって、割る前にそっち側の計算完了させないといけないだろう
3*3と
3(1+2)は違う
後者はわけたらいかん
3(1+2)でひとまとまりの数値だ。
ひとかたまりであるということを明示するために×の省略が行われるってことかな
そういえば、なんのために省略するのかは教わってなかった気がする
混乱しやすいかも。
算数しかやってないなら答えは9
ここを先に計算するものだと理解できないと文字式や因数分解を出来ない
係数扱いなら1になる
総じて問題がよくない
「Exceptions to the standard」のところにちょこっと書いてあるが、うーむ。。。
これもこれで日本のとは違うな。
2(1+2)は掛け算じゃないよ。 係数だよ
係数の答えを出す計算過程でカッコ内の数値に対して掛け算が行われているだけだよ
それを済まさずに手前の6から先に割るとか、数学の知識が無さ過ぎるだろう
かっこ内が優先なんだよ。
何でそういうルールかは知らないけれど。
3(1+2)にして分配法則使って
3+6=9って答え出したんだけど。
違うのか?
6
ー(1+2)=9
2
関数電卓君は 分数で書くと
6
------
2(1+2)
という計算をしている ※2(1+2)を1つの割る数と考えてる
高校~大学の数学やっていけてるのか?
因数分解とかどうするんだよ
かっこがある場合は、かっこ内の計算が優先されるんだよね。
これを思い出した。
これ出題者がドヤ顔で間違い書いてるだけなんじゃね
分配法則で(2×3)or(3×2)なんだよ
係数はそれ以前の話
そもそも係数はどれのことをいってるんだ?
係数は定数項なら定数項自体だと思うが?そもそも定数×定数の数式の一部が係数とか言うのがおかしくないです?
任天堂ファンのみんなは大正解!!!全員満場一致で9!!!
ゴキちゃんたちはちゃんとおべんきょしまちょうねーwwwww
>>52
その説明が一番しっくりくる。
もとい「どれが正解でも構わない。」
つまり「どれが正解でも関係ない。」
結局「そんなことはどうでもいい。」
結論「あきますた」
6になんの?
その考えでも2(1+2)を一纏めとして考えるんだけどね
これで計算式じゃなく計算の解だから
というか2(1+2)=2×(1+2)として考える場合は必ず2(1+2)を一纏めとして考える
これを2と×(1+2)にわけて考えることなんて絶対にありえないぞ
9派の人は分けて考えているならそれがどこで使う計算法なのか教えてほしい
ソースがあるなら考えを改める
()は一つの文字として扱うって習わなかった?
教科書にも書いてあることだぞ
それに省いていいって言い方は解く側に対しての言い方だよね
そうでなければ×を省略した意味が無いから
わりと出尽くした感あるよな
算数でならったように省略としたら9だし、数学の一次式4X÷2X=2のような考え方にしたら1ですよね。
定数だし、前者のほうが自然だとは思いますが、そもそも問題の書き方がおかしいし、2つの考え方が言えれば正解かと。
優先順序に従って計算すると
最初に(1+2)を計算して6÷2(3)
次に2(3)を計算して6÷6
最後に6÷6を計算して1が答えになるんですが…
1で断定してるのはまだしも、まぁそれは理系だろ
このサイトそんな低年齢ばっかりだとは思わなかったわ
理系のオタクばっかりだと思ってたのに、ちょっと見方改めるわ
()内はまとめて考えてるけどそのまえの2までなぜまとめる?
そもそもXとかYとか変数もなく()以前を係数と扱う根拠は?
6÷2×(1+2)と書かれていれば間違う人は少ないだろう。
ちなみに、6÷(2(1+2))と書けば答えは1。
通常の計算式で書こうとするとどうしても表現出来ない→しょうがないから特別に認めます、ってのを括弧で表現してるんだよ
そんなんが集まんのはあっちの某掲示板だろうな
そんなの習った覚えないぞ 数学ならあるけど。
さんすうでは掛ける記号の省略なんて習いません
数学では色々な理由で×記号を省略して表記する場面があるけど
その全てが、一つの塊として扱うという意味合いで×記号を書かないんです
9以外の人は数学やり直してこい
そもそも係数表示としてxを省いてる
数学的に考えたら尚更答えは1です
できる子=1か9で迷う
普通の子=1
バカ=どうやったら1になんだよwww
答えは1だろーが
算数の概念ではこの問題は計算できないはず。
よって、算数で9と答える奴は完全に間違い。
算数では乗算器号は省略できません。
やたら目につくな
定期的に流行るよな
xの省略ってのも中一の文字式で出てくる話
xや・と区別してこれは係数ですよって意味で省略する
たぶんたしか
足し引き掛け割りくらい小中高でマスターしろよ・・・
>>631
せやな
6÷2×(1+2)と書かない出題者が悪いでFA
すると、算数として出題した人が馬鹿という結果になるなw
9派もそれに対する反論を言ってほしい
6÷x(1+2)=1 だとx=2になる
つまり6÷2(1+2)=1なんじゃねーの?
つまり2(1+2)ってのは6ってことにしかならないから1になる
算数の知識と前提で解くのはおかしい
バカ目
でも何かの『なぞなぞ』かと思って
変な計算しまくって悩む自分がいた。(笑)
わからんやつは小学校からやり直せ
省略記号は1グループ扱いだから優先して計算しなくてはならない。
9になると言っているのは表記間違いを理解していないだけ。
× 6÷2×(1+2)=9
○ 6÷(2×(1+2))=1
なぜ他の人の※を読まない
中高生達が記事の計算問題の答えを見る。
↓
9!9!と言い張りだす。しかし、一部では1と言う声も。
↓
それを見た中高生達が罵倒する。
↓
しかし、問題がおかしいので答えはどちらにでもなる。
↓
結果、中高生達顔赤失笑w
できる子=1か9で迷う
普通の子=1
バカ=どうやったら1になんだよwww
バカ=どう考えても9
バカの頭は算数で止まってるくせにドヤ顔で笑うわ(笑)
因数分解とか係数とか知らないんだろうな〜
この時間帯に餓鬼共はいないんだと
xの省略は一纏まりとして扱う
中一の最初期に習う話じゃ無い?
1になるよ
2(1+2)={2*(1+2)}なのかってことだが、
普通に考えれば後者だと思う
問題が誤りと考えることも出来るけどその場合は"解けない"が正解だよ
()は文字式の様に扱って×を省略してもいい、と考えると1が解になるけど
9という解が導かれる考え方は存在しない
だから正解は9だと言ってる人にはちゃんと考え方も言って欲しいんだけどねえ
その考え方は間違っているという反論への再反論も
この式、何に使えるの?
何を表せる式なの?
(2+1)=1×(2+1)
係数1は省略している
商や積は先に順に計算する
よって9
イデアルってのは簡単に言うと()の中の数字の整数倍の集合って意味(だからこの場合マイナス入れた9の倍数)
つまりイデアルさえ導入すればこの計算は省略記号の計算順序など考えなくても何も矛盾はない
なぜならイデアルで割るという計算もイデアルを割るという計算も存在しないからな
……いや、まぁただ矛盾がなくなるだけなんだけどさ
積の省略された2がもうあるからそれは使えないな
おお、なるほど。
今度から気をつけやす
つか数字と()の間で掛け算するのは勝手なルールなの?それはそれとして決まりごとでなかったっけ?
バイト1人と開発2人分のおやつ(1人2個ずつ)から、
捻出すればええんや!!
…って、カヤマさん言ってる。
1、もしくは「問題が悪い」
どう考えても1
最初の6と2をa,bに置き換えて考えると分かりやすい。
a÷b(1+2)=a÷3b
これにa=6 b=2を当てはめて戻すと、
6÷(3×2)=6÷6=1
流石にこれで分からないのは小学生だぞ。
教えてくれた人ありがとう
中々おもしろかった
判りづらいわ
男の子一人と女の子二人で作るグループが二つあります
六個のリンゴを全員で分けると、リンゴは一人いくつもらえるでしょう 答え1個
男の子一人と女の子二人が居ます
子供たちにリンゴを六個ずつ、カゴに入れてプレゼントしたいのですが、一つのカゴにはリンゴが二個しか入りません
カゴは全部でいくついるでしょう 答え9個
結局、出題者がおかしいという事ね
あんた、すげえや
文字式でないのに×を省略して書いた算数って、質の低いクイズでしかないなw
答えは9だよ 1は不正解だよ ってとこまで含めて釣りなんじゃねーの?
A÷B(C+B)を計算しろって言われたら
A÷{B(C+B)}で計算しないと不正解なのは万国共通
それ右辺無いから方程式になってないよ?
全体見えてないあほっこです
論点が違います。
これなら1だな
691のこと?
「算数できて数学できない」
だからすぐに9だとわかったんでしょう
文字式について習った時点で小学校の数式は0次の多項式になるわけで…。
知らなかった当時の形に似てるからって、当時おそわった幼い解釈に戻る必然性がない。
この記事ってそうやって書いてたら誰でもちゃんと分かるから問題がおかしいって話じゃないの?
6÷2(3)=
3(3)=
3×3=9
6÷2(1+2)=
3(1+2)=
(3+6)=9
割り算先でも( )先でも9になるんだが
どうやって1になるんだ?
俺もそう考えた
だから、2(2+1)という形になると思うよな
6÷2(1+2)=
6÷2(3)=
6÷6=1
2(1+2)は一つの係数なので分母が2(1+2)、分子が6 と考える
もし展開するとしたら6÷{2*(2*3)}だぞ?
中学で文字式について習うときに、係数・因子・項の話をみんなちゃんと聞いてるはずだよ。
項の乗除算と係数の乗算は「計算方法が同じでも結合規則が違う」別々の演算記号なんだけど、
「どちらもかけざんだからとりかえっこできる」という屁理屈で小学生に退行すると9になる。
中学生でも1と分かってるのな
ここで9と主張してる奴らは小学生だったのか
さんくす。すっきりした
でもって2年前のネタで2年前と同じ論争が繰り返されてんのな
もしかして小卒?
1. 係数や因子はドット・で表す。これは省略してもよい。
2. ドットは乗算と同じように計算するが、因子は項より強く結合する。
3. 文字のない文字式は0次式である。
よって、中学生以上ならば 6÷2(1+2) を0次式 6÷2・(1+2) と解釈し、 6÷{2×(1+2)}=1 と評価する。
6÷2(1+2)だと
(1+2)に係数2があるから割って1
表記ミスだと言いたいのだろう。
なんで上の式では括弧の中を普通に足し算してるのに下の式では分配法則使ってんの?
上の式分配法則で6÷(2+4)にして1にならないというなら人生詰んでるぞ・・・
どっちが正しいとか以前にどっちの答えにも辿り着けないと奴はこの問題の意味が分かってない。
ちゃんと紙に書かれてたら皆分かるだろう
物理の単位は分子になる方はマイナス何乗って表記するもんだから
いまとは全然別じゃない?
そこまで自分で書いといてそう思うならもうそれでいいよ。
こんな問題が出来なくても使う機会がない人間にとっては無駄知識だからね。
6÷(1+2)=6÷1(1+2)
=6÷1×(1+2)
=6÷1×3
=18
6÷(1+2)=6÷3=2
よって数学的に矛盾が生じる。したがって背理法により、仮定が間違っているという事が証明された。
a(b+c)は先に計算しなければならない。 証明完了
中学までの知識で証明するとこんな感じか?もちろん、数式がおかしいってのが一番の原因だが、あえて解こうとすると1だな。
わかる奴は1
つまり中学までの知識しかないやつは1って答えるわけか
> 6÷2(1+2)=6÷2×(1+2)=9であったと仮定する。
> 6÷(1+2)=6÷1(1+2)
> =6÷1×(1+2)
> =6÷1×3
> =18
> 6÷(1+2)=6÷3=2
0点
仮定にもとづく計算を自分でミスして矛盾が生じてるだけですね^ ^
>6÷2(1+2)=6÷2×(1+2)=9であったと仮定する。
>6÷(1+2)=6÷1(1+2) ← この変換のせいで本題とは関係ないところで矛盾が生じてるだけだぞ?
>6÷2(1+2)=6÷2×(1+2)=9であったと仮定する。
>6÷(1+2)=6÷1(1+2)
↑
この変換はむしろ
6÷2(1+2)=6÷{2×(1+2)}=1 と考える側の仮定に基づく変換の仕方だろ
6÷2(3)
6÷6
1
・・・なるほど
1で間違いないよ。
小学生レベルの知能と思われたいなら9でもいいけど。
括弧や文字の前の係数の1は省略しなさいって習うはずだよ。
逆に言えば、省略をちゃんと書き直してから計算しても、問題があってはならない。
係数の1を追加して数式に齟齬が生じちゃいかんのよ。
もちろん、文字式じゃないのに×省略すんなっていう話だけどな
>>─────
2(1+2)
こういうことか~わかんなかった(泣)
>6÷(1+2)=6÷1(1+2)
と変換して勝手に矛盾作ってたけれど
じゃあこれを6÷(1+2)×1と変換したらどうなるんですか^^?
難しい・・・
>係数の1を追加して数式に齟齬が生じちゃいかんのよ。
そもそも この題での6÷2(1+2) の()の隣にある2は係数じゃありませんよ^^
(1+2)をxとおいて
6÷2x=x分の3=(1+2)分の3
……=1
(´;ω;`)ごめん。俺は小学生からやり直しっぽい(笑)
自分頭良いと思ってんだろ
こんな計算できても頭良いわけじゃねぇんだよ
1か9とか議論して「俺すげぇこといってるわ」
みたいな気分か?
マジきめえ
え?
この程度の討論にもついていけないの?
>1か9とか議論して「俺すげぇこといってるわ」
この程度のこと自慢にもなりませんよw
被害妄想丸出しのコンプレックスの塊さんには自慢してるように見えちゃうんだねw
おお!わかりやすい!
1だ。
わからんやつはわかるやつに素直に習えばいいし
わかるやつはわからんやつに教えてやればいいだけなのに
別に知らないことは恥ずかしいことじゃないんだからさ、素直になりなよ
2(1+2)で意図的に×を抜くと、意図的に抜いた意味は何となる
×じゃダメな意志が働くから
それ背理法までつかっちゃった上に間違ってるやつだよ
そもそもこの題での6÷2(1+2) の()の隣にある2を係数と考えてる時点で間違い
これは文字式の6a÷3aとかではないのだから
その場合の答えは2だね。
ただし、係数を入れただけで異なる計算方法で異なる数値が出てくるというのが問題なわけだから、議論には影響を与えないけどな
>>759
係数じゃないなら、そもそも×の書き忘れで式が完全に間違ってるという結論でおしまいなんだw
2×3と23は違うという話で終わり
学力下げてるのがどの年代か…
3、4、6、7=10
9999=10
この左辺に×÷-+をいれて10になるような答え教えろ
俺にはできなかった
>2×3と23は違うという話で終わり
おばかさんは黙った方がいいと思うよ^^
今回の問題は 6÷2(1+2)ですよw? 読める^^? ちゃんと()で識別できるようになってますよねw?
6÷2 3 なんて書き方をしたせいで問題が生じたわけじゃありませんからww論点をすり替えてごまかそうとしないでねw
×を入れると不都合があるから抜いた。
それだけ。
なるほどー。じゃあ、この式が文字式か否かという話だとすると以下のようになるのかな。
文字式は乗算の記号(x)を省略できる
乗算の記号を省略してあるので文字式と考える
答えは1
文字式は乗算の記号(x)を省略できる
式に文字が入っていないので文字式ではない
文字式ではないのに乗算の記号を省略しているので式が不正
解なし
出典「6÷2(1+2)=?」という小学生レベルの問題? 大勢の人が「1」と答え半分以上が不正解
ってわざわざ書いてあるのにいまだに「1だ!」と主張してるバカは何なの? そんなに馬鹿アピールしたい痛い子なのw?
最近は、そんなに学力低い連中が多いのか。
問題としてオカシイ
そうだね。
・答えは1
・答えは9
・問題がおかしい
このすべてについて納得できない人は勉強不足。
答えは1つじゃない。
学者によっても答えが違うらしいしな。
()の前の数字もしくは変数に後ろの()内の値が掛かるという事
しかしその前の記述に÷があるから処理順序がおかしくなる
あくまで記述に従うのなら割り算より掛け算を先にする事になるが
これもし試験で回答欄でこんな解き方したら不正解だぞ
だから、ただの計算式で文字式じゃないのに、×の省略なんて表記はしちゃいけないんだよw
確かに文字式でも数字同士で演算記号の省略なんてやってはいけないけど、あれはあくまでも例だよ
文字式じゃないのにそんな表記をしているということは、2()というのは2×3を23と略してるのと全く同じなわけ。
ちゃんと2×(1+2)と書かなければならない。
納得したから俺的にはそれでいいや
しかし、間違っているとはいえ、数式で曖昧さを表せるもんなんだな
そういう意味では面白かった
マジで1って言ってるやおるやんw
中卒かわいそうww
高卒乙
いや、これプログラムで書いちゃダメだろw
もう馬鹿はほっときなよ…
中卒さんかわいそうw
自分の理屈で反論できないのか。Google頼りとは情け無い。
1+1が2になるのを理屈で言えよっついわれてる気分w
おつかれさんでした
情報学卒、数学卒の友達に聞いてみた
二人とも答えは「1」でしたが
でももう飽きてきた
つまり問題がおかしい
知能レベルの差はあきらか。
と、また煽ってみる。
>>728みたいに背理法まで使って「1だ」と主張してるやつはおもしろかったよw
6÷2(1+2)
D÷C (B+A)
だっていう人はいないでしょ
この出題者はこれは算数だからといって無理やりルールを変えてるんだよ
大体途中式で
6÷2(3)とか書く時点でおかしいだろ
算数がしたいなら最初から6÷2×(1+2)って書けっていうだけの話
出典「6÷2(1+2)=?」という小学生レベルの問題? 大勢の人が「1」と答え半分以上が不正解 - ガジェット通信
だが・・・
正しい答えは「9」となる。
元記事に書いてあるやん んで正しく計算できないやつらが問題が悪いと主張 ← 今ここ
"正しい答えは「9」となる。"
ガジェット通信が ”正しい” の?
同じ所に
※数学者数名に話を聞いたところ人によって解がことなり、そもそも問題の書き方がおかしいという指摘があった。
と書いてあるのは見えないの?
問題が悪いって言ってる人の主張する内容を、自分なりに解釈て箇条書きで書いてみな。
書けますか?
9って答えたアホ乙
俺の答えは1、または9、または問題が不正のため解なし
数字を言って当てるのが目的ならそれでいいよ
3とaの間にはみえない×が入ってるから
3(1+2)の()はaに該当するって考えていいだろ。
つまり答えは9にしかならないと思う。
むしろ答え1になるって計算法が思い当たらんw
なんか昔お釣りのやり取りでそんなこと言ってるアホがいた。
数学だと答えがいくつもあるから、買い物した時のお釣りも答えが1通りとは限らないってめんどい奴がいたなぁ。
どんな順序で買っても、合計金額は必ず同じだろ。
つまりそういうこと。
2択問題にて
「俺の答えは○か×だ!(ドヤァ」
出題者「そ・・・そうですね^^;(だめだこの子はやくなry)」
それはただの屁理屈だろう
>>819 >ふつうに9
もうね・・・・^^;見ててかわいそうになってきちゃう
問題のすり替えですね。わかります。
6÷a(1+a)を解きなさいという問題なんですが…
そりゃそうだ
じゃあなんで答えが違ってくるかと言えば、計算間違いをしてるかそもそも式が間違ってるかの2種類しかない
つまり、捉え方によって答えが変わってくるような式を立てた奴が悪い
答えが9以外ないって言ってる奴は論外
係数2(1+2)と解釈すれば2(を最優先で計算するので1になる
だから問題が悪いということ
まず、普通の数式と、aとかbとかが入ってる「文字式」とで乗算記号のルールが違うという事らしいよ。
普通の数式では乗算記号を省略できない。
文字式なら省略できる。
したがって、この式が文字式かどうかで答えが変わってくる。
もっというと、乗算記号を省略してるのに文字が入っていないので、式がおかしいという解釈になる。
一周回って馬鹿が優越感に浸れる
文字式ではないのに×を省略してるのは正しいということ?
9かなと導きだすのが本当にかしこい子
その意見にはなっとく
なぞなぞの答えにマジレスしてるのと同レベル
こんなの端からひっかけ目的なんだからどこでひっかけてくるのか予想して回避くらいしろよ
ひっかけるためにそうしてるんだからね
問題にならない この出題者がしたいのは「ひっかけ問題」
問題がおかしいのは当然なんだよ
そうじゃなきゃ誰も間違えずひっかけ問題にならない
あえて答えをだすなら9だけど
すくなくとも何の違和感も感じずに9と
即答できる奴は理系じゃない
なんでこういうのが定期的に出てくるんだ...
掛け算は順番変えても解は変わらんけど、割算は変わるだろ。
二分の1と、割る2を混同する本物のバカが問題が悪いとか
がんばれ
大勢の人って曖昧な表現だな。多分小学生辺りに聞いたんだろ。
台湾のfacebookコミュニティにはそんなに小学生が多いのかね
大人が多いと思うな
ただし算数に×省略の概念はないので、1が正解でFA
9とか答えてる奴はちょっと恥ずかしいぞ
(1+2)を文字に置き換えると凄いことになる。
それと
6÷2×3の答えはなーんだ?(笑)
間違えたかーwと思ったが
結局1で正解と言うことか?
つか、理系大卒で9の回答は正直やばい。
ある意味バグっすわ
後者なら絶対9だと思うけど。
それより、文字ないのに×省いてよかったっけ…混乱してきた。
2(3)は2×(3)じゃなくて2・(3)だからね
でもふつう(慣例的に)数字だけの数式の時は・使わないから問題がおかしいんだけどね
> ×と・の違いが判ってる人なら答えはちゃんと1になるです
> 2(3)は2×(3)じゃなくて2・(3)だからね
> でもふつう(慣例的に)数字だけの数式の時は・使わないから問題がおかしいんだけどね
> >> 884
> > ×と・の違いが判ってる人なら答えはちゃんと1になるです
> > 2(3)は2×(3)じゃなくて2・(3)だからね
> > でもふつう(慣例的に)数字だけの数式の時は・使わないから問題がおかしいんだけどね
>
>
式はおかしくないと言い切れる一般人がいることに驚きだ。。。
> ×と・の違いが判ってる人なら答えはちゃんと1になるです
> 2(3)は2×(3)じゃなくて2・(3)だからね
> でもふつう(慣例的に)数字だけの数式の時は・使わないから問題がおかしいんだけどね
2・(3)がなぜ1になる?
なぞなぞの答えにマジレスしてるのと同レベル
こんなの端からひっかけ目的で数式あいまいにしてるだけなんだから
どこでひっかけてくるのか予想して回避くらいしろよ
> 延々と同じ議論をしておれ
入ったりしてすまん
脳内で6÷2×(1+2)へと変換してあげる位の度量が試されている
ひっかけるためにそうしてるんだから
そんな糞問相手に問題が悪いと言ったところで何の解決にもならない
馬鹿正直問題悪言答同端目的数式予想回避
> 2(1+2)分の6なんだから1じゃないの?
6(1+2) 分の2だろ
きもwww
> 安価できてない奴が粘着君だな
> きもwww
まとめブログリーダーで安価するとこうなる
習わねーよ
数字だけの算数で、×の記号省略したことなんて普通はないはず
あとこれはひっかけ問題だから~って言ってる奴、
つまりは算数や数学の式としては落第ってことだよな
これ間違える奴小学生の時何してたんだよwww
日常生活にも支障出るレベルの馬鹿だなwww
そうだよ
だからこんななぞなぞレベルの問題をいちいち学者なんかに聞くとかお門違い
文字式でも無いのに乗算記号省略されると
89が8*9なのか八十九なのか分からなくなるだろ?
算数のなぞなぞとして出題してりゃよかったんだろうが
計算問題として出題しちゃったらダメ
試験だと出題ミスで全員正答扱いじゃないかな
問題として間違ってるなんて馬鹿正直に正論かざしたところで無意味なんだよ
なぞなぞの答えにいちいちマジレスしてやる必要はない
馬鹿さがにじみ出たコメントですね
さて、○○さんは今どこにいるでしょう?
A,自分の席
B,自分の席以外
という日本語での問題といっしょ
数式の曖昧さを楽しむためのジョーク問題
意図的に抜いたのなら1が正解
少なくともあなたよりはマシですから
くだらない因縁つけてこないでください
()式は文字扱いになるに
>なんで6で割るんだ?
a+bを先に処理するのは当然として次にやるのはnとカッコ部分の展開だろ…
根拠もなくwww
違うぞ
カッコ→×÷→左から順番
×が入ってねーんだよ、なんで抜いたのかといえばそっちを先に計算したいからだろ
はいはい
キチガイDQN乙
くだらん因縁つけてくるな
×を省くことと計算の順番は関係ない
そう思う
2(1+2)を1つの項として先に計算させたいから×を抜いた。
数式を見慣れていると、このように解釈してしまう。
nはカッコにかかってるからそこ処理だろ
因縁つけられるような事を書かないことだな。
無理やり答え出すなら1で合ってるんじゃないの?
ありがとう
×がしっかり描かれてればな
なんで×がないのかといえば2(1+2)で一つの塊だから
○AxB=AB
×AB=AxB
xの省略は積であることを示す
積とは乗算結果であり崩すことは出来ない
別に因縁つけられるようなことは書いてませんが?
わざわざ因縁つけてきたってことは自覚してるんでしょ?www
DQNさんwww
=6÷2(1+2) (乗法記号の省略)
でここから続きを出題の場合だと困る
だから数式ってのは誰もが分かるように書かなくちゃいけない
これが1か9か多くの人に悩ませる時点でこのような式を提示しちゃダメ
なぞなぞやジョークとしてはよくできてる
どう考えても1だろ
これ間違える奴小学生の時何してたんだよwww
日常生活にも支障出るレベルの馬鹿だなwww
6÷2×Aだったら答えは9になるが
xの省略はそれ自体が意味を持つから
いや実際には「省略」なんかできない
そんなことしか出来ねーの?www
これだから馬鹿なキチガイDQNは嫌いなんだよ
条件が曖昧すぎてどんな答えでも出うるってのは出題として失格
例えればいきなり「まるいものってなーんだ?」って言われてるようなもんだよ
まるいものならどんな物でも正解になってしまうし、同時に定まった答えはないって事になる
てゆか、この手の話題もういいよ。馬鹿の言い訳聞くのもウンザリだ。
どうやったら1になるんだよwwwとかほざいてるのが2番目にばか
自分が何を書いたかわかっただろ
「()の外か中が文字の場合だけ」って習わなかった?
まあ嘘は付いてないんだろうな
半分以上は答えが出せると思って考えてるもんな
高校数学の一番の基礎なのに
んなこと習うかよw
2√3は定数同士の積表示だぞw
何がしたいの?
絡んでくるな馬鹿
数字だけの計算式で×の省略習ったの?w
1になる計算方が逆にわからんがな~
誰か教えて
ニコニコ大百科で6÷2(1+2)と検索するがよろし
実際はどちらかが数学のルールを見落としてるだけ
やっと思い出した
だったらたしかに半数以上の人間が解けないな
これは証明問題であって数字出すものじゃない。
これ。単にこれだけの話。
正答を一つに確定出来ない数式は数式とは言わない
じゃないか?
これが
(6÷2)(1+2)
だったら9になるんだけども
理学系統なら1とかになるんじゃないの? 単純な数学なら9かもしれんけど
うん、だからこんなのを書いてはいけない。
計算式と文字式の表記ルールをゴチャ混ぜにして
オマエラを混乱させてるだけ
つまり
表 記 自 体 が お か し い
これ以上の議論は無用
問題でググって一発で出るってことは有名な問題だったのか・・・
ドヤ顔で9とか答えたバカは中学生からやりなおせカス
それで計算すると1だよな
これだったらどうなんの?
> ※157で終わってた
いや、終わってない
どっちも1になるはず
はちまの過去記事にも同じ?内容のものがあったような気がする
そのコメが間違ってます
6÷2(1+2)と6÷2×(1+2)は違う計算
2(1+2)はこれで一纏めであって分けてはいけない
で終わりだよねこれ
> 「1」って答えちゃった奴が顔を真っ赤にして反論してる。って聞いて
2(1+2)は一つの項だから答えは1になる
もうここは1派しかいないよ
> 割り算掛け算から先にやって、割り算掛け算が式にいくつかある場合は左から解いて行くんですよ
何度も言わせるな
2(1+2)は一つの項だから離すことは出来ない
6÷2√3とか8xy÷2yとか解いてみろやw
一応()の部分は文字式の様に使えるよ
あんまり美しいとは自分も思わないけど
他にも数値式でも×省く例としては上で言われてる√の計算などがある
> >>996
> 6÷2√3とか8xy÷2yとか解いてみろやw
まだ算数で習ってません
どーでもいいじゃんこんなのwwwwwww
6÷2(1+2)の2()が係数扱いになるか?で1にも9にもなるんだから
問題が悪いという結論でそろそろ落ち着けよ
それなのに未だに9とか答える人って・・・
まず()の中から計算する場合と、
()の前についている数字を分配法則してからと、
そういうので答えが変わりそうですよね。
順番さえ知ってればどうにでもなる
日本人なら出来るだろ
問題の問題点を答えろって問題だな
わざとそうなるように書いてるそういう問題だ
作った奴の目的は見事に達成されてるな
「問題が曖昧でどちらとも取れるため欠陥問題、あえて決めるならどちらかといえば1が妥当」
ただし台湾では正答は9に決めちゃったらしいし、もうどっちでもいいだろアホらしいって感じだな
1しかねーだろ、9なら×を記載し忘れましたって話だ
何度言わせる気だ?
2(1+2)はこれで一つの項なの
項って分かる?
素直に前から計算して行って9が正解
文字式を嫌という程解いたであろう奴なら
()から先に計算したくなる
それで慣れちゃってるからねえ
その上で1か9かを論じるならまだしも、
1が意味不明とか言ってる奴は中卒以下
ちょっと6÷2√9の計算して貰っていいかな
ましてや、1か0か、今回の場合は1か9かだが、2つの答えが対立する場合その傾向が強まる。
焦点がどこにあるのか、対立する相手が言わんとすることは何なのか、論理的思考を養うにはもってこいの、まさに数学らしい問題だと言える。
文字式以外で×が省略されるケースなんかあるのかと
でなきゃ×を省略しちゃいけない
以上
馬鹿かおめえ
乗除に順番なんかねえよ
どうしても答えるなら1って結論出ただろ
算数は国ごとに違ってもいんだよ。日本の場合算数と数学の移行期の特殊な問題。
小学生及び高校生以上は解ける必要はないが、中学生だけは間違ってはいけない。
実際に出題される。コレの答えは「1」
日本では乗算の省略は優先されれると教えられる。「×」ではない。
実際に算数から数学に移行するときにはその方が論理的に連続性をもって処理ができる。
つか、いい加減昔に議論に成った問題だ。
6÷(2a+2b)=x
これにa=1,b=2を代入して
6÷6=1
x=1となる
類義語:日本語でおk
ここに答えあんじゃん
この式の違い分からん奴は去ったほうがいいわ
2√9と2(1+2)では計算の順序が違うと言うのなら
その根拠を出来ればソース付きで教えてほしい
あと6x÷2xも計算して貰えるかな
どの順番でやっても答えは変わらん
6÷2(1+2) = 6÷2×(1+2) = (6÷2)×(1+2) = 3×3 = 9
6÷2(1+2) = 6÷2×(1+2) = 6÷(2×(1+2)) = 6÷(2×3) = 6÷6 = 1
後者は右側の掛け算を優先していることから間違いだと分かる
ただ人間の脳が掛け算のほうが結びつきが強い=先に計算するって誤認しやすいんだと思う
お前ら覚えとけよw
3a² とか言いそうだなそいつ
お前らもさんすうごときで得意気になるな
何度も何度も言われてるけど2(1+2)で一つの項です
だから6÷2(1+2) ≠ 6÷2×(1+2)です
これは中学数学で×の記号を省略するときの計算について必ず習います
これが出来ないと文字式も因数分解もルートも計算出来ないから
そこだよね
普通、数字だけの式で2(1+2)なんて書かない。
つまり数字だけの式に文字式のルールを持ち込んじゃってるわけで、
その場合の、
’×’が省略されていると考えて「6÷2(1+2)」を「6÷2×3」とするのか
もしくは
文字式の一つの項と見て「6÷{2(1+2)}」とするのか
ここの定義というか優劣というか、それが無いのでは?
ほんとに知りたいならニコニコ大百科で検索するといいお
この記事はコメント稼ぎなんだお
だから、日本では乗算の省略は優先されると教えられるんだよ。中学数学というのは、小学校の算数とも違う、
高校以降の完全な数学とも違う不完全なもの。
項の概念を算数からの移行で考える時に、乗算の省略は一つの項として考えるよう制定された。
その方が、乗算の順番は問わないという数学のルールにスムーズに移行できる。
実際に中学ではこの問題出るんだから嘘言っちゃいけないよ。算数は各国共通でなくてもいいの
そもそも、数学では「÷」なんて使わない。
小学校でやった事すら分からないとか
そんなにはちまのためにコメ稼ぎをしなくてもいいんだよ?
中高ではなくて、中学のみね
高校ではそもそも÷なんて使わないだろう
答え:1の計算方法も分からないような人が他人を批判してるよ…
いやいやいや
でなきゃ省略したらあかん
素直に 6÷2×(1+2)
と書くべき
以上
実際にそうなんだから仕方がない。
「÷」なんて不完全なものを使いながら数学に移行するための苦肉の策なんだから仕方がないよね。
つか、ここの中学生。1年生で教わることなんだから、自信をもって先生に教わったと言わなきゃ駄目じゃねーか。
計算方法が分からんって奴は数学の知識以前の問題だわ
9と答える方が多かったら、正答は1でしたって言うだろこれ
断言してるなこいつ
違ったらどう責任取るわけ?
今年来年再来年いろんな受験するやつがいるけど
「÷」が不完全てどゆこと?
そこらへんの話聞いたこと無いんで教えて欲しいっす
言い方変えると単純w
÷も/も(一部地域では:も)数学的にはまったく同じ意味の記号だよ
さんすうと数学での除算の表記の違いは分数で表記する様になること
で、PCなどの分数で書けない媒体だと/を除算の記号か分数の記号かで混乱がみられる
まずコレ解いてみろや
あとは数字当て込むだけだろ?www
1で確定してるのに
数学では乗算の計算は順番は問わない ○
失礼
むしろ使わないとダメだろ
数学まともにやってるなら
×が省略されていると項として捉えてしまい、
先に2(1+2)をやっておかしくない
てか関数ないときって省略していいんだっけ?
あの…その長いコメのどこにも÷と/の違いを何一つとして言ってないんですが……
数学では別に問題ない。日本の算数ではそもそも乗算の省略はやらない。
ただ、数字が並ぶ場合は完全に省略せずに。2・2・4・5= のように、略式記号はしっかり書く。
横からだが
2=1×2
だから
6÷2=6÷1×2ってのはおかしくないか?
普通数式を代入するなら()でくくるんじゃないか?
だから
6÷2=6÷(1×2)になるんじゃない
自信満々に9ってのが逆に痛いわ
代入って考えがそもそも数学の考えなんだよ。
まぁ、その例は良くなかったね。一見意味がなくなる
>>1085
1068です。理解できました、ありがとうございます。
その他にも2=1×2 であることを考えると、
6÷ 2(1+2)=6÷1×2(1+2)
という滅茶苦茶な式が成り立ってしまう。
それはない
6÷ 2(1+2)=6÷(1×2)(1+2)
だろ
おまえバカだろ
そりゃ式めちゃくちゃにんるわw
演算子が入ってくるとどこまでで区切ってるのかわかりにくいから
ちゃんと()で括るか、もしくは分数で表記しろって言われる物だぞ
混乱の元だから安易にこれでも伝わるだろうで書くなって言われる
そうじゃない。代入の概念いれてるから、代入だと思うのはわかる。説明の仕方が悪かった。
×だけで構成されてるから、それらは同じ式でなくてはならないんだよ。
その問題算数と数学をもあえて混ぜてるの。君が指摘した意味では正にそれを狙った式だが、
算数か数学の計算どちらかに統一すると同じになってしまうから適切ではなかった。
6÷ 6=6÷3×2
という問題にしないといけなかったね。
数学で÷という記号がゆるされるならこの2つの計算結果は同じで無くてはならない
お前は正解だぞ
悪いけど何を言ってるかさっぱりわからんぞ
6÷3×2は 6 ÷3 ×2 と考えるものだし
6÷2(1+2)は 6 ÷2(1+2) と考えるものだ
これ算数なら9だが数学なら1になるな・・・
()が最優先じゃなかったけ?
6÷2(1+2)
6
= ―――
2(1+2)
算数では演算記号の省略がないので式が間違いになるだけ。
6a÷2a=3a^2って答えてたの?
6÷{2×(1+2)}=1 って書くわ
だから、「÷」が分母と同等であり、「×」が乗算の省略と同等と考えれば、そうならないでしょ。
算数と数学をグッチャグチャにすると、齟齬が生じるという説明だよ。説明が下手で悪かったよ。
少なくとも日本では1102で正しい。
1と答えるやつの気がしれんわ
ありがとう、なっとくしたわ
これの答えが分かれるってことはまだまだ数学を教える側も未熟なのかなぁ…
よくわからないけどさ
9派だと6a÷2aは6×a÷2×aではなく(6a)÷(2a)になる
>>1110
(6÷2)×(1+2)=9じゃなく6÷2×(1+2)=9でええやん
AGE-1はあるけど
AGE-9は無いだろう?
(´・ω・`)だからおまいら落ち着け。
別にいいよ。中学生でなければ。
そもそも、これは日本では中学生以外解けない特殊な問題。
そお? 日本だけじゃないよ。÷が()を多用しないと正確に表現できないできそこないの記号だから
その問題は世界共通。
それに台湾の問題で、数学への連続性を考えれば日本の答えの「1」の方が矛盾が生じない。
数字同士の掛け算で×の省略が許されたら、
10+10=?
1×0+1×0=0
とかいう意味不明な答えが許されちゃうだろ。
だからこれは問題の書き方が悪い。
だから()内が係数なんだろ、普通に使うぞ
かけ算が成立するためには、大前提がある。
たとえば〈一匹あたり、必ず二つの耳〉のように「1あたりの量が一定」でないとかけ算という計算は成立しない。
一匹あたりの耳の数が違った場合、かけ算という計算はそもそも全くできないのである。
つまり、かけ残とは「1あたりの量が一定のときに全体の量を求める計算方法である」ということがいえる。
(1あたりの量)×(いくつ分)=(全体の量)
。
9だろ ← バカ
問題が問題だろ ← ドヤ顔
イメージとしては
一匹 三匹分
(1本) (1本)(1本)(1本)←6本
(1本) (1本)(1本)(1本)
1あたり量 全体の量
かけ算の概念を考えるときは、このような縦と横の面積をイメージするとわかりやすい。
これ以上でも、これ以下でもない(1あたりの量)が決まったものを、いくつ合わせた全体であるか。
と言う計算なのである。
ああ、日本の算数はそれで順番固定するよね。
数学になってから混乱するからヤメロって。
(1あたりの量)×(いくつ分)でも (いくつ分)×(1あたりの量)でも同じだって教えなくなった。
わり算とは果物をみんなで〈均等〉にわける計算である。
わり算は〈不均等〉に分ける場合には計算できない計算方法である。
わり算が成立するためには、均等にわけるという大前提があるのである。
つまりわり算とは、かけ算でいう(1あたりの量)を求める計算である。
(全体の量)÷(いくつ分)=(1あたりの量)
他にもあるが、これがわり算という概念の基本である。
じゃあどうすんだよw
この「かけ算」「わり算」の概念はこのように固定されている。
そしてこの二つの計算は逆演算の関係にある。
しかし実は
「足し算(加法)」(summation)
「引き算(減法)」(subtraction)
の概念は、固定されておらず、そのイメージはひとつでないのである。
果物を分ける方法は、明確に2種類あるけどなw
全く違う分け方をする。
「1」はバカとはいえないだろ。日本では「1」以外有り得ない。
中学の時教わったことを覚えていれば解ける。
まぁ、これは算数側から思考すると9、数学側から思考すると1という間違えさせるように意図的に作った問題だけどね。
最初に「÷」の直後の数字だけ分母になるという算数の特殊ルール思い浮かべた人間は「9」となるし
「÷」は分母という数学側の思考を始めた人間は「1」になる。
「足し算」と「引き算」はイメージが固定されていない。
2+3=5
と足し算が表記されていたとして、これを読むとき。
①「2と3を加えると5」
②「2に3を加えると5」
という2人の人が現れるのである。どちらも5に違いなのだけど、イメージは違うのである。
そろそろ問題が問題と気がついた奴が増えてきたから
何を今更w
とか言っとけ
①の「と」の方を「合併」
②の「に」の方を「添加」
と呼びます。
小学生ですか?^^
①の方の「合併」は、「一つのビンに、同じ角砂糖を左手で2個と右手で3個入れる」イメージです。
②の方の「添加」は、「一つのビンに同じ角砂糖が2個入っていて、手で同じ角砂糖3個をさらに入れる」イメージです。
5-2=3
と表記されていた場合
①「5から2をひくと3」 (これを「求残」)
②「5と2の差は3」 (これを「求差」)
という、別々のイメージが式から発生します。
そうです「かけ算(乗法)」(multiplication)
これだけは、他の何にも変化しようがない概念なのです。
そして問題式に戻りましょう。
これが1になる方法なんて存在しないぞ
日本ではね。そもそもこれは数学の問題ではないので、こんなへんてこな数式は世界の国々で答えが異なって当然。
÷をつかうならきちんと()を多用しないと数学では通用しないし、複雑になるので普通使わない。
海外は「1」と「9」に別れるんだよな
要は省略した×を補完するかしないかによる
wolframalpha の答えは 9
やべー、これからは入力の順序に気をつけないと、、、、、、
はあ・・・バカ文系がよく言うわ
選挙でも身に染みてるだろう?
9だな
頭が固いおっさんか逆にゆとりかねw
そうでしょうな。
普通は、自分が9と思おうが、1と思おうが、みんなの意見を聞いているうちに他の答えもありだなと思うはず。
それが出来ないのは頭が固いか、他の理屈が理解できないかのどちらかでしょう。
1って答えるのは基本的にアスペ
この問題は日本では中学でしか存在しなくて、「1」だからね。
本当は算数の問題だけど、一応数学と名乗ってるのに、数学と答えが食い違うような真似しちゃマズイだろう。
台湾では小学生の問題となってるから、「÷」の基本の働きに縛られて「9」なんだろ?
こいつはバカってこと?
つまり9
小学生の問題なら乗算の略式記号や省略がでてきてはいけないんだよ。
中学でしか扱わない特殊問題。
高卒なら1
大卒なら問題にけち付ける
横からだが俺略式小学生で習ったぞ
>まぁバカ多いのは仕方ないねと1の数を見て思う
>9以外に何があるというのか
>1って答えるのは基本的にアスペ
>1とか小学生からやり直してこいwww
>1は無いわー
>ん?9だろ
このように何も説明出来ていない。
問題のレベルに気がつけ
割り算したの?
数字とかっこの間に何も書いてなかったら×だって中学校で教わったぜ?
おーよしよしそんなに悔しかったんだな
1だぉぉぉぉぉぉぉおおおおおおお!!!
「項」という概念があって、×が省略されていたらその部分を1つと考えるので先に計算する。
そう
中学レベルなら9で正解
表記が紛らわしいとかなんとか。
2を係数と考えるかどうかで……。
な?
数式の作り方は、÷よりも()の前の係数を優先するため
そうだっけ? 十数年の前の学指導要綱には載ってないし、そんなものを教えるように成ったとは考えづらいが
先生が独断で教えたんじゃね?
省略は教わってないはずだよ。それは確実に中学の範疇
そこで乗算の省略時は計算が優先されると教えられる。
という世間の常識に気がつけるとこの問題の意味が見えてくる
子持ちだとわかりやすいよね
×9
○出題がおかしい
駄目です。中学生はピンポイントで「1」なんだよ。
小学生は答えられない。高校生以上はどっちだっていい。
あぁ÷と略式が共存する問題を最近どっかで見たようなと思ったらそれか
寝るか
問題自体が不思議な形だから解なんじゃなくてこの問題が見れるのはいつなのかから考える問題なんだろうなとは思ってた
B A K A
うn
算数では省略しない。
÷があるし 計算が混乱するのは仕方ない。
問題に問題があって
成立していないとかなんとか。
D O A H O
こんな風変わりな式が平然と見れるのはほんとうに限られた範囲の世代に限られるからな
自ずとそうなる
これだったらどうなんの?
算数の問題で、1か9かは文科省の設定次第なんだけど
一応、日本では算数から中学の移行期に実際に問題が出る。
算数から数学へ過程で不連続があると望ましくないから、文科省が定めた「1」でいいと思ってるけどね。
数学理解できない君は驚くだろうな
で、答えはなんだよ
まぁ、こんな問題出さなきゃいいという考えは正しいと思う。
で答え出た。
終了だな。
「÷」やねん
マジメに数学としてみたら計算できないもんなコレ
計算する必要すらないということに気がつけるようになるとハナマルシールもらえるよ
むしろこんなゴミ問題作って多数の人に時間を奪ったことが許されない
フルーチェで例えると、
「2=フルーチェ原液」、「(1+2)=牛乳」
2×(1+2)=原液と牛乳を並べてある。これから作りますよという状態
2(1+2)=混ぜ終わって完成したフルーチェ
いや、傍らで眺めてたのしみたいだけだけど、、
日本では実際そう教わる。この問題がでてくるのが中学だから、
分配法則やら、乗算の順番は問わないやら色々問題が出てくるからね。
9と計算したら。因数分解とかとんでも無い話になる。
数学的に厳密に生徒に教えられると理想なんだけどね。難しいだろうね。
先に割り算するか掛け算するかで分かれるんやな
俺も1だと思ったわー
だから、この問題は÷に注目してそう考えてもいいし、
2(1+2)が項として考えなければならないと考えてもいいしどっとだっていいんだよ
両方間違ってるとも言えるし。÷と項が混合している異常な問題。
ただ、中学生は間違えてはいけない。出題されるから。
>これって文字式じゃないから2とかっこの間に×をいれることは出来ないと思うんだけど
>解が異なり、そもそも問題の書き方がおかしいという指摘があった
と言う事は、正解は両方ありえると言う事になるわけで、
「半数以上が不正解」って事が根底から覆る、全く意味の無い話って事になりますよね?
何が言いたいの?
出題者が解は1つだと勘違いしている人って話?
それとも、結局解が1つで成り立つの?どういう記事?
無価値。。
もし、謎掛けならば、答えは ? かなとw
このスレを読んだら、実は間を取って4か5が正解なんだと今気づいたわ。
論語の中に出てくる「中庸」の概念を理解してないと解けない高度な問題だと思う。
安心しろ。
全国で最下位を争う超低学歴高校卒のオレですら9だった単純な問題。
たかだかクラスで1番とか書くなよ恥ずかしい。
なんでかって言うと、数学的論理展開が不可能になるから
まぁ、9って言ってる人は小学校で習ったことをしっかり思い出してるだけなんだけどね。
算数としてみれば9でいいんだけど、数学側から敢えて答えなければならないのなら1しか有り得ない。
算数の欠陥を露呈してる、ある意味いい問題だよ。
見方を変えればポアンカレ予想に匹敵する難問なのではないか
って考えれば誰にでも分かる、単純な嫌がらせ問題だな
四則演算記号っていうのは記述式解答における「言葉でのつなぎ」に相当するんだよ
小中の算数ってのは、数学に至る以前であって丁寧な記述の解答をやってる段階なんだよ
だから算数と数学混ぜると位相がずれて矛盾が生じる
それが、算数側からみるとありえるんだよ
6÷2A=
6÷2×A=3Aとなる
ちなみに、数学がわからみるとそれで正しい
÷なんていい加減な記号使った上に、数学的に成立するまで()を付けなかった結果齟齬が生じる
この問題は前に議論した時は算数の教育的意味と効率的な指導方法に終始したけどね。
全員、この問題の意味がわかっていたから。
というかこれはそういう問題。そこまで考えないのなら確かに無意味だね。
中学生ならとりあえず「1」の計算方法覚えとけ。それ以外なら忘れろw
9と答えてるやつらは6÷2√9をどう答える?
だから理解度を確認するために(6÷2)(1+2)と6÷2(1+2)が並んでにテストに出たりしてた。
…気がする。
式に関するルール間違えたら計算出来ても答え間違うわな
6÷{(2×1)+(2×2)}だろ。
6÷(2+4)
6÷6=1
1ではないか。
と思ったが、しっかり左から計算すると
3(1+2)
(3×1)+(3×2)
3+6=9
9でした。
×が省略されてるのは確かだけど、こう考えるのが自然な気がする。
長年数学やってきた感覚的に。
「2(1+2)で、1つの項」
おk、すっきり!
こういうの好きー。
切符時代はやりまくってたわw
答.
6×7/3-4=10
(9×9+9)/9=10
いや、まぁそれで正しいけど。日本の中学ではという話で、他の国で通用するかは別なんだよね。数学は世界で統一されているが、算数は統一されているとは限らない。中学で一つの項として考えろと教えてるだけで、そもそも、数学で÷なんか使わないし、万が一使ってたとしても厳密に表現するまで()を付ける。こんないい加減な数式はありえない。日本では中学、紛いなりにも数学で扱うから、多項式、分配法則、乗算の順序のを問わないなど数学との連続性を保つために、そう考えて、答えは「1」なんだけど、これ小学生で習うとしたら、話が違ってくる。÷の意味が幅を利かせ、乗算の省略は×でしかない。と考えないと児童の理解が難しい。そう考えると合理的な解は9になる。日本は乗算の省略は項として扱い、計算が優先される。とされているから数学的観点からすると算数からの理解が進みやすく合理的で、「1」と教える日本は良い。と思ってたんだけど、よくよく考えてみると誤魔化して、そもそも出題しないほうがいい気がしてきた。
( ) > 乗除 > 加減
1だよ
あとは
左から順に解くもんだ。
だけど、普通はこんな書き方をしない。仕事の文書では特にしない。読み手に「書き間違い?」と思わせてはいけない。
わかる人は1
解法見て納得しつつもどことなく違和感が拭えないのは何ゆえw
此れを解いてくれ
6aは(6×a)と扱えって事だろ
AB=(A×B)
6÷2×(1+2)=9
まあマジレスしても何の意味もないけどな
つまり半数以上の数学者は能無しってことか
そういう引っかけ問題。
そうです。「わり算(除算)」(division)も実は、足し算・引き算と同じく複数のイメージを持っていて、これがわり算の応用です。
わり算の基本の概念は〈等分〉から、かけ算の逆計算である(全体の量)÷(ある1つの量)=(いくつ分)ですが
6÷2=3 この式は人によって
①「6を2等分すると3」 (これを「等分除」といいます)
②「6には2が3個含まれる」 (これを「包含除」といいます)
どちらもしっかり〈等分〉されているのですが、イメージが複数現われるのです。これが隠された、わり算の応用。
しかし「かけ算のイメージはただ一つ」
数学が駄目で1と答えたのなら、お前は算数すら出来ないということだ。算数で解けばこれは9にしかならない。
>>1259
>>1260
乗算の省略は項として扱い、最優先で計算されるという中学生のみの特殊ルールが有る。
項を扱わない算数から数学へ移行するための便宜措置
>>1264
半数以上なんてどこに書いてあるの? 数学者でも回答がわかれて数学として考えると問題がおかしいと言われただけだ。
数学者が算数混じりの中学の問題なんて覚えてるワケ無いだろ。
6÷2*(1+2)
項で考える場合
6÷[2(1+2)]
になるってこと?
というか、項が身についてるかついてないか。
少し考えて9にしたのなら問題ない。
×と乗算の省略は働きが違うって問題だから、それは微妙に正しくないね。
そもそも算数からの移行で÷を使わなければいけない中学数学のみで起こる問題だから
÷の働きに縛られると、項の概念の理解の理解が進まないという理由で作られたルールでしょ。
本当に数学なら÷なんか使わないから問題が起こらない。使ったとしても6÷[2(1+2)]の様に厳密に表記するしね。
この式は表記の誤りにより
計算不能となる。
したがって解は存在しない。
(´・ω・`)僕は文系なんだよね。
1かと思ったけど式が破綻?しているから
解は存在しない。
文系なんで許してちょ(笑)
記号変えたってルールの問題だし
6÷2(1+2)=6÷2(3)=3(3)=9
下は書いてて凄く違和感があった。
6÷2(1+2)=6÷2(3)=6÷2×3=9
と考えるからだよ
2(3+4)=2×7の塊と考える。
算数と数学が混ざってるからね。
数学者の先生達が
この式をどう捉えて
解くんだろな。
答えは1
6×1/2(1+2)=1
V(^-^)V (完)
がんばろうな!
お前がそう思うんならそうなんだろう、お前ん中ではな。
前者で考えた場合1になり,後者で考えた場合9になる.
したがって問題の設定が厳密ではないということ.
解法が一意に決められない問題を出す出題者もいいかげんですね。
A=1+2
6÷2A=X
X=1
で終了だろうが。この問題を6÷2×Aだから答えは9って答えるのか、馬鹿か?アホか?いい加減にしろ。
----(x+y)=z
b
かな??
= 6÷2(3)
= 6 ÷ 6
= 1
になるじゃないか
もし、答えが9になるなら、式を直さないとだめだ
(6÷2)(1+2)
=(3)(3)
= 9
じゃないのか?
それか成立していないかどっちかだ
数字と(の間に×は入るの?
あなたは頭がイイ。
俺「式の変換も左からなんだけど・・・なんで先に右の×付けてるの?」
くだらなすぎる
2(1+2)÷2(1+2)=?
って事だろうがっ!
常識的に考えて。-
ちなみに÷を/に置換すると1が正解なのがわかる。
(´・ω・`)だから1と言いたいのね?
わかります。
解が9になる方の式って数学上だと使えないし、
1になるように統一して教えるべきじゃねの?
1+2=3
次に6÷2=3
そして、答えが出た出た2つをかける。
3×3=9
これでおkかな?中学ほぼ行ってないから断言出来ないけど、かっこ付いてる場合はかっこの中を最優先に計算してってのと、かっこの前に×や÷など無い時わそこわかけ算
こんな感じに習った気がwwてか小学生でも出てくる問題だよね確かこれww
↑ってなること忘れんな1になったおバカさん
たしかにww
アホだなほんとw
(1+2)
がどうして分母の方にかけてあるんだよwww
そのアホっぷりに拍手。
高校、大学を出てから出直しな。
こんなインチキな記事で、こんなに反応する人がいると
うはうはだな。俺もこのコメントで加担してしまった。
算数では、掛けるの記号(x)は省略しないのだ。
小学校で×の省略なんて習ってないと思うし
だからこそ×省略した場合って文字式を考慮したうえでの係数扱いになってそう
前コメで数値しかないから文字式関係ないって言う人は
×省略できるのはどんなときでもって思ってるの?
俺は良く分からないから、数学者に教えてもらいたいな
左の式ならば(A×C)/(B)
右の式ならば(A)/(B×C)
1になる人は勝手に右の式に変換している気がする
AをB×Cで割るのではなく、AをBで割りCをかける
何にしても式の書き方が悪い
自分の行いに疑いを持たないのが一番愚かだと思う。
B(C)の部分は項といって、ひと固まりで扱わないといけない。
A×B≡ABではないの。
この問題は突き詰めていけば、1が正解になると思う。
本文に「正しい答えは9」とか間違いなのにドヤァって感じに書いてあるから、俺9になったはって人が増えてるのかと
中学の時にちゃんと習ってるはずなんだがなぁ、年代によって習ってないのかな?
>1342
B(C)は展開する時B×Cではなく(B×C)となる
A÷(B×C)ならA÷BCに書き変えることができるがA÷B×CではAC÷Bになってしまい問題文と同じにならない
算数で×の省略はできないから答えは1な
右辺に9入れて両辺に2(1+2)掛けたあとの計算式書いてみてくれ
さて、どんなトンデモ言い訳が出てくるやら
はるか20年近く前だが小学校でこう習ったしなぁ
数学においてあらゆる命題に”解釈”というものが存在する
一般に扱われる定理は普通"任意の解釈"で成り立つようになっている(トートロジーという)
特にこの6÷2(1+2)は2通りの解釈ができる
つまりある解釈では1が正解であり
ある解釈では9が正解である
トートロジーではないから1が正解とか9が正解とかはないんだよ おわかり?
”任意のxに対して条件Aがなりたつyが存在する” というのは
”任意のxに対して条件Aが成り立つ”yが存在する というのと
任意のxに対して”条件Aが成り立つyが存在する” というのでは異なる解釈で
数学では通常このような異なる解釈が起きないように一意的な問題を提示しないといけないが
この6÷2(1+2)という問題はそうではない
1だけが、または9だけが答えというのはやぼなこと
これで言えば分子は6、
分母は2(1+2)
ていうか、2とかっこの間に半角あけてるのが
わざとらしい誘導だろ
それ以前に1と9以外の答え言ってる奴はもっと馬鹿っぽいけどな
何度も言われてるが、この式が決められたルールによって成り立ってない時点で、決まった1つの答えにはならない
この式を近いルールに当てはめて考えるなら1か9になり、一番近いルールを当てはめるなら1になる、というだけ
何故1になるのかわからない、と言ってる奴は凄く馬鹿っぽく見えるぞ
と回答するのが正解じゃないのか?
ルールをどのように認識しているかどうかの問題だよな。
だから、決して難しい問題とかではないし、解けたから賢いとかでもない。
馬鹿じゃねえの(嘲笑)
はい、終了。
上にもあるけどそもそも出し方がおかしいんで成立しない
これを9と言い張るのはなぞなぞと同じくらい低レベル
こんなん俺でも:(;゙゚'ω゚'):ってなるわwww
>間の「かける」を省略するって事は2と(1+2)はもうセットになってしまってる。
出、出~www自分ルール発動奴wwwwww
×、÷は左から計算
このルールで計算するだけじゃん
6÷2(1+2)
→6÷2×3
→3×3
→9
1です
左から計算って言ってんだろカス
A÷BC = A÷(B×C) ≠ (A÷B)×C
A÷BC = A÷(B×C) = A÷B÷C
A÷BC =A÷B×C 勝手にかっこつけんな
※1377
(1+2)をaと置き換え、6÷2aとするとわかりやすい。
6÷2a=6÷2×a=3×a
答え9なんだろ?
1って言ってるやつはいい加減間違いを認めろよ。答えが9なんだから
ふむ、それなら
15a ÷ 3a = 5 でなく
15a ÷ 3a = 15 × a ÷ 3 × a = 5(a^2)
こうだと言いたいの?
○ 15a ÷ 3a = 15 × a ÷ (3×a) = 15 × a ÷ 3 ÷ a = 5
文字式じゃないからどうこうってツッコミ入れるなら分かるけどなぁ
答え9と言われたから9って・・・
自分の頭でしっかり考えてみたか?
9とか言ってる奴はゆとり。
数式ってのは分かりやすく現したひとつの形だろ?
わかりにくいやり方にしてどうすんだよ・・・。
6÷(2x+2Y)じゃなかったっけ?
だったら1。
これを
3(x+y)とするなら9だけど。
9って書いてる人が間違いだろ。
6÷2×(1+2)と6÷2(1+2)は違うよね。
6
―――――=1
2(1+2)
って考え方があって、後者の方が多いってだけだろ
でも「普通に計算したら9」派も多いってことは、いつからか「●(▲+■)=●×(▲+■)」って教えるようになったんだろうね。
計算機によって答えが違うのも確認した。AndroidアプリのHandyCalcでは※1386さんの挙げた後者の表記で計算され1になる。
「式を同じ項でまとめてくくる」以外の掛け算で×省略したことなんてないし
していいって言われたこともないんだけど。
1派も9派も仲良くしようぜ
6÷2x(1+2)と6÷2(1+2)をそれぞれ分数に置き換えて計算してみろよ。
前者は分母に2だけがきて、答えは9。後者は2(1+2)が分母にきて、答えは1。
この違いな。
分かりやすいように付け足すと、2x(1+2) は 2(1+2) とは = じゃないってこと。
もっと分かりやすくいえば、6÷2(1+2) は 6÷{2(1+2)} に置き換えられる。
計算はカッコ内からするのが決まりだから、答えは1。
OK?wwww
盛大に間違ってますおwwwwwwwwwwwwwww
ワロタwwwww
バカ丸出しwwwwwww
2aは一つの項なんだから、6÷2aにおいて、2とaはバラして計算しねぇんだよwwww
おwつwかwれwwwww
>>1394読んでやっと理解できた。
もっといえば6÷2(2+1)=の左辺も単項式じゃね?
まぁ、答えが9になる問題で途中式こんな書き方したら間違いなく減点されるがw
9は無理やり感が半端無い
どこから×が出てきた?ww
ズレてるのが問題かなぁ・・・でも項は中学で習うから、普通は知ってる。
ナカーマ
6÷2(1+x)=9 と仮定して
3(1+x)=9
(1+x)=3
x=2
「9」が正解と出ました…この検算合っているのかな?
×記号を省略するなら割り算は分数で表すだろjk
だよね。9になると言ってる人って
XやYが出てきたときに躓いてそうw
>数学者数名に話を聞いたところ人によって解がことなり、そもそも問題の書き方がおかしいという指摘があった。
と書いてるだろ。
お前らは数学者よりも偉いつもりなのか?
容易に他者を見下す人間が頭が良いわけないだろう
2を()の中に掛けるのが最優先って教わったけど。
だから2(3)ってするのがそもそも間違いなんじゃ。
6÷(2×1+2×2)になるわけで、そこから()内の計算をする。
よって答えは1。
2×(1+2)=2×1+2なら( )を付ける意味がない、という事
( )内を先に計算しないなら、何故( )を付けるのかの説明が必要だ
正解:9と言っている諸君、説明してくれ
記憶違いでは?
・が入ってるはずだし、本当は入れないといけない・を入れてなかったとかじゃないの?
要はそれぞれ分けて考えれば良いだけ
混乱する奴は関数とか作れない
5は俺だけのようだ
>計算のセンスが無いな(キリッ
2(1+2)でひとつのブロックのような気がしてならない。
・6÷2m だったら、答は「3m」なのか、「3/m」なのか。
(元ネタの趣旨だと前者らしいけど、かなり違和感あるね)
これはy=6÷2x
でx=2+1の時に
y=6÷2x=9
と言ってるのと同じじゃん
1+2=3
6÷2=3
3(3)=9 ■()と整数3の間に何も無い場*が省略されてるとみなす
理系→1
数学専攻→文字式以外の乗算記号は省略できないので問題に不備がある
どちらも正解の場合9=1がなりたってしまう事に気付いてないwwwwwwwwww
どっちも間違いじゃないと思うけど・・・
「10÷2(1+2)」というのを考えてみた。
これは頭の中で15と計算した時、すっきりした。
10÷6が割り切れないから。
6÷2(1+2)=1という答えが出たのは、学校のテスト問題の答えで1というのが多かったから、1という数字にスッキリ感をもっているからなんじゃなかろうか。
この手の問題は日本人なら当たり前のように出来ると思ってたんだけど・・。
括弧で綴じられていないんだから、除算より乗算を優先する理由が全く無い
おんなじ例で、「このへやではきものをぬいでください」→「この部屋では着物を脱いでください」と、「この部屋で履物を脱いでください」この両者が、対立したとき、誰が悪いかってことでしょ。まぎらわしいんだよ。問題作る側が。
なんか納得した。
数式では乗算記号が省略できないって義務教育で習うよ
答えは9でも1でも無い
義務教育忘れてる人多すぎ
しかしたった一個の(簡単そうな)式にこれだけの論争
この問題考えた奴だれだよ、わざとなのかミスなのか・・
故意だとしたら、大・大・大成功!!!だなw
文字が無くても()や√などの記号があれば省略はできる。
そういうソースが見つかってニコニコにある。
数学の知識がある人とない人で答えが割れるのは当たり前で、両者に共通の言語になる必要はない。
当然正しい公式を使えば1になるわけで、公式無視で間違いの9という答えも認めるというのはおかしい
9は間違いということになる
「問題がおかしい」ですね。
理由は明快で、数学には
『文字が絡まない()内の式は数字扱いされる』
というルールが存在するからです。
ということは、文字が絡まない(1+2)は数字であり、なおかつ 2も数字であるため、
2 と (1+2)の間の × は省略してはならないんですよ。
これを省略すれば、上で1446さんが言っておられるような、意味不明の式が出来上がることになりますね。
それにしても一体、誰がこんな問題を考えたのかは知りませんが、なんとも人を喰った問題ですよね。
俺知ってて就職できないのなんでだよ・・・
でも静岡大の教授の例題で12AB÷4Bという問題があるよ?
確かに自分も学生の頃同じようなの解きまくった。
厳密な話をすれば、「間違い」ということになりますね(笑)
でも、これは間違いようもない式であり、しかも計算法を説明する途中式ですからね。
途中式なら問題をどういう経緯で解いて、数字をどう処理するかということは、自分は勿論、説明を受ける側も、
ちゃんと意味を追っていれば理解できているでしょ。だから別に問題はない、という話だと思いますよ。
6÷2(1+2)=?から、随分、難しい話になっていたんですね。
では私が書いた『文字が絡まない()内の式は数字扱いされる』という言葉だけでは不適切でしょうね。
ただ、逃げと言い訳をしますが、その辺りの詳しく踏み込んだ所までは申し訳ないですが分かりかねます。
というのも、ただでさえ一般的に知られていない(使わない)ルール。
(このルールを利用した問題にはどの問題集でもお目にかかったことはありません)
以前何かの本で読んだ限りの説明で、それを解説するサイトなどの情報源があまりにも乏しいからです。
でも、私がニュアンスとして認識しているのは、『文字や記号等が絡まない()内の有理数の式は数字扱いされる』というところですね。
おそらく間違いではないと思いますが、断定はできないです。ごめんなさいね。
ただ「分からない」ですが、「以前そういう解説文を読んだことがある」ということです。
だとすると、日頃扱ってる問題などと見比べた場合、6÷2(1+2)=?の場合、2(1+2)という記述は不適当だと言ったまでですよ。
何より、ここで喧々諤々の論争を展開して相手を論破すれば、それが数学の真理になるというわけではないのですから、
「卑怯だ逃げた」と取られても仕方ないですが、無益な論争を避け、よりその道に熟達された方に下駄を預けさせて頂きます。
私は数学教師であって、数学者ではないですからね。
そういう人間をはめるためにわざと作った問題って感じだろ?
昔も全く同じ問題に対する議論があったけど、これは出題者がアホってことで結論でてる
「1と9のどちらでもOK」←これはありえないと思います
6÷2(1+2)=1
6÷2(1+2)=9
1=9
「解なし」←これも無いと思います
ググると分かりますが数学における「解なし」は、そういう解であって
もし問題に不備があって答えが出せない場合は「解なし」とは言わず「問題に不備がある」と言わないと混乱します
×とあるプログラミング言語ではこう処理される
×カシオのなんとか計算機では9だ
×こう教えていた、習った
○この教科書にはこう書いてる
一般には、最初に割る数2(1+2)の()内が0でないことを確かめるために、()内を計算しないといけません。
これをやらないで済むのは、6÷2(1+2)のように、割る数に含まれる()内が0でないことがすぐ分かるときだけです。
また、a×b=abや2×√3=2√3と書いてあるなら、本来、×と省略された×の計算の優先順序は同じです。
これらの原則に則って等位の考え方で6÷2(1+2)を計算すれば
6÷2(1+2)=6÷2×(1+2)=6÷2×3=9
と求まります。
多分、実情としては、一々6÷(2√3)なんて書くのは面倒だから、
本来6÷(2√3)と書くべき式を6÷2√3と書いているだけでしょうね。
まあ、+と÷を何かの拍子で見間違えて、6+2(1+2)を6÷2(1+2)と、写し間違えられたり捉えられたりした
ということは十分あり得る話ですね。
あと、可能性は低いと思いますが、6÷2×(1+2)を6÷2(1+2)と書き間違えられた
ということもなくはないですね。
何れにしろ、x=1+2と置き換えたりせず、計算だけでゴリゴリ6÷2(1+2)の値を求めるなら、
等位の考え方を採用せざるを得ません。
計算途中でx=1+2と置き換えるようなことは義務教育ではしない筈ですね。
その等位の考え方が出来ないなら、答えはなく、問題自体が悪いです。
等位の考えというのは計算順序が同じと考えて計算する方法です。
台湾の義務教育で出されたこともあり、6÷2(1+2)を計算せよ、
という問題は見たところ義務教育で習う問題に似ていますね。
高校で習う計算途中でx=1+2と置き換えるようなことをして考えてよいなら、
普通に答えが1にもなるので、問題自体が悪い、で終了です。
まあ、細かくいえば、沢山の人にとって、数学に共通言語としての数学であること
を要求することは、少し無理があると思います
(6÷2√3という式も、厳密にいえば6÷(2√3)と書く必要があるんです)。
>>1478の1番上の行の
>等位の考えというのは「計算順序」が同じと考えて計算する方法です。
は
>等位の考えというのは「計算記号の優先順序」が同じと考えて計算する方法です。
の間違いでした。失礼致しました。
「÷、×、省略された×の計算の優先順序」と書いた方が分かり易かったかな。
基本的に、等位の考え方は、忠実に式の書き方通りに従って優先順位を決めて計算する方法です。
この考えだと、大抵の人にとっての6÷2(1+2)という数式は6÷(2(1+2))と書くことになります。
大抵の人は暗黙のうちにa÷bcをa÷(bc)と捉えていると思います。
等位の考えではa÷bc=a÷b×cとなります。
また、この考え方を採用すれば、6÷2(1+2)は書き間違いではなくなります。
大抵の人は、暗黙のうちに6÷2(1+2)=6÷(2(1+2))と仮定している可能性があります。
大抵の人にとって、等位の考え方は変わった考え方ですので、この位で止めときます。
いわゆる論理的にはなりますが、書き方が面倒で、空気を一切読まないような考え方だと思って下さい。
出てくるソースは1派のばかり。
a÷bc=a÷b×c ? 等位がどうか、台湾はどうかは詳しくは分かりませんがここは日本で
日本の数学の教育課程では a÷bc=a÷(b×c)≠a÷b×cなわけです。
まあ空気を読めない考え方ですので釣りですね。
a÷bc=a÷b×c
この考え方をする時点で数学を教える資格はありません
話は難しくなりますが
a÷bc=a÷b×c
のような考え方が出来るしっかりとした厳密な数学はあります。
この数学だと等位の考え方で考えることになります。
大抵の人は、それに触れる機会が全くなく、知らないのだと思います。
逆に
a÷bc=a÷(bc)
のような考え方が出来るしっかりとした厳密な数学があるのかどうかを知りません。
つまり、義務教育の数学は、厳密な数学で考えたとき
理論的整合性が取れなくなっているんです。
個人的見解を書かせて頂きますが、
大抵の人のように考えると、2×(1+2)=2×3=6と簡単に計算出来るので、
6÷2(1+2)のような式は書くべきではないです。
混乱が生じるだけです。
普通に考えたら、教育を受ける人はまだしも、
2×(1+2)=2(1+2)と計算するようなことは、普通の感覚ではあり得ないと思います。
値を求めるにあたり、意味のない計算をしているだけです。
教育を受ける人はまだしも?
教育を受けていない人に合わせろというのですか?なぜ下のレベルにあわせねばならないのか?
数学における基礎中の基礎です。
よく人によって捉え方が違うから、このような書き方はすべきでないという意見もありますが
これは問題です。当然問題の解答には正解とその他の誤った答えがあり、謝った捉え方で解いて
正解と違う答えなら×、なのに問題が悪いとか?
ひっかけなどがあるのは当然なのだから、ひっかかった自分が悪いとはなぜ考えないのかわからん。
静岡大の教授の話にもあるようにA÷BCはA÷(B×C)が正しいが、よく間違った答え方に多いのが
A÷B×Cと解いてしまうのがある・・。教科書ではあまり触れられていない。
要はこの解き方を知らない人間が、多い間違いの考え方をする人が文句を言っているだけです。
あ、そのレベルの話はもう終わってるよ。
それは文字式のルールじゃん。
その文字式ルールを今回の数式に適用していいのかどうか、そういう事が記述されてるソースを探してんだよ。
※1475
0割算を回避する為に場合により計算順序を変える説。
すまん、スルーできなかったw
35(35-15)とか。
()内を文字と同様に扱うというソースもある。
とっくにニコニコでは1で結論出てる。ここが遅れてるだけ。
では逆に適用してはいけないルールのソースは?ないでしょ?
少し専門的知識が必要になりますが、
a÷bc=a÷b×c
という考え方は出来ます。何も矛盾は生じません。
>>1492
0で割れないことは、数学の基本中の基本です。
忠実に、この大原則に従って考えたり計算したりしているだけです。
a÷bc=a÷b×c この考えが正しいのなら
a÷bc=a÷(b×c) これは当然間違いということですよね?
例え可能であっても、計算するにあたり意図的に
2×(1+2)=2(1+2)とか、35×(35-15)=35(35-15)
と書くことは、不自然な考え方です。
意図的にこういうことをする人は、多分、将来どこかで躓きます。
0で割れない事は小学生でも知ってるけど、
>>1475さんは0で割る事を回避する為に、あるいは分母が0にならないかを先に確認する為に、
計算順序を場合により変更してるよね。
そのルールは初耳だなあ。
そもそも計算において0割算を回避する必要は無いから。
0で割らなければいけない時点で解が「不能」になるだけだから。
÷をどう定義するかによって答えが変わります。
÷という記号はそういう記号です。
普通の人のようにa÷bc=a÷(bc)と定義するなら、
論理的にはa÷bc=a÷(bc)=a÷(b×c)となり正しくなりますし、
等位の考え方でa÷bc=a÷b×cと定義するなら、÷、×、省略された×の優先順位は同じと考え、
論理的にはa÷bc≠a÷(bc)=a÷(b×c)となります。
このように、同じ計算記号でも+や-、×とは違い、÷は定義によって扱いが変わる記号です。
そう捉えておいて下さい。
>>1499の
>高校で、定理の条件で分母が0でないときに
>割算が出来ることを保証する定理は習いませんでしたか?
は
>高校で、定理の条件で分母が0でないときに
>割算が出来ることを保証する「条件がある」定理は習いませんでしたか?
の間違いです。申し訳ありませんでした。
あと省略された×は×、÷と同等の優先順位で計算とありますが
省略された÷(分数)は先に計算するんですよね?都合よすぎです。
説明では絶対に信用できませんのでソースをお願いします。
等位の考え方のソースは、忠実に式の書き方通りに従って優先順位を決めて計算する方法らしいのだが、今、省略された積についても、定義されているのですか?そして、文字式に入るのですが、それを学んだ時点で、等位の考え方の一部(省略された×の計算の優先順序)は消えるのですか?それとも、数値式は残って、文字式は消えるのですか?私は、それを習った覚えはありません。せいぜい、×の記号は省略してもよいくらいしか学んだ記憶がありませんが。
1497 0で割る事を回避する為に、あるいは分母が0にならないかを先に確認する為に、計算順序を場合により変更?こんなことしたことありません。するとしたら、影響ない範囲で、やってますが、原則は前からです。
例えば、8×6÷(2-2)×(1+2)であれば、2-2を先にやって、割られる数が0なので、解なしとすることはありますが、こういう意味でなら、やります。ただ、ふつうに、
8×6÷(2-2)×(1+2)=48÷(2-2)×(1+2)=
解なし×(1+2)=解なし としても自然だと思いますが…(この、二つは等式としては成り立たないが、便宜的にあらわしていると思ってください)
こんなの混在してる式の定義なんて見たことねぇよ
→高々0次式の問題。
それは、どう区別するべきなの?
そんなことしたら話が余計に混乱するから、ここでは普通に考えて計算した方がいいと思うよ。
全部とまではいい切れないが、専門書でも+や-より×や÷を優先させて、分配法則は
a(b+c)=ab+ac、つまり普通の人にとってはa×(b+c)=a×b+a×c
と書いてある。+を優先させたら
(a(b+c))=(ab)+(ac)、つまり普通の人にとっては(a×(b+c))=(a×b)+(a×c)
或いは
a(b+c)=(ab)+(ac)、つまり普通の人にとってはa×(b+c)=(a×b)+(a×c)
みたいな式になるが、こう考えると(普通の人から見たら)余計話が合わなくなる。
0割算の答えは「解なし」じゃないってば「不能」だってば。ぐぐってみ。
×省いちゃだめでしょww
でも、無理やり解くとしたら、
6÷2(1+2)
=6÷2+4
=3+4
=7
配分したらカッコのけろバカども
じゃあ、省略しちゃダメのソースは?
でも、等位の考え方で計算したら、普通の人と合わなくなる。
6÷2(1+2)を等位の考え方で計算しなさいなら9であるが、
6÷2(1+2)を解けといわれたら、どうするんだい?
1512 0除算の話は、別のところでのほうが良いような。もう、あまり議論しません
解がないのは△のほうだろーが
わかったもうこの話はしない
すみません。俺が間違ってました。色々調べたら中学生以下は「不能」を「解なし」と言って良いそうです。
しかもスレチで申し訳ないです。もう書きませんのでご安心下さい。m(__)m
引っ掛けの受け狙いだろうね。
小学校算数程度では別段当たり前の問題で、大人をターゲット
だろうな。
くだらない。
6x ÷ 3xを2x^2と答える奴はいないだろう
と思ったけどプログラム屋とかはそう答えそうだな
誰か物理的に説明してくれ。
で、これの答えが出ることで何が解決すんだよ。
÷の記号を使っている国が悪いって考え方もできるけど
2aと2×aが別物であるって教えているのはちょっと聞いたことが無い
この場合、答えは「どちらも正解」であり、出題者は出して欲しい答えが得られるように問題から曖昧な部分を
取り除く必要があるわけよ。
6になった
あるよ。省略された積についての解釈が最大の論点じゃん。何で意図的にそこを避けるの?
今って、中学で展開勉強しないのか?
カッコ外すところからやれば普通に解けるだろ。
割算も省略して分数の式にして書かなきゃってこと
6÷2(1+2)=6÷2(3)
=6÷(2×3)
=6÷6
=1
どっから4が出てくるんだ?
ただあくまで日本の数学の常識を元にやってるから海外だと1の場合も9の場合もあるってことね
そのあと、6÷2(3)の6÷2を先に計算するか2(3)を先に計算するかで
9になるか1になるかが別れる
2(1+2)を先にやってるんだな
2(1+2)を、「2x1」と「2x2」としたんだろうな。
すると2と4になる。
そうして出来た2と4の、2だけを先に使って6を割るから3が出来上がり、
残った4と足して7・・・
って、思いっきりバカな人じゃ、そういう間違いはしないんだよな。
ある程度自分の考え方が出来上がっているからこそ、誤りを
補正するのは骨が折れるんだが・・・。
→6=1×2(1+2)
になるんだけど?
6になりますか? なりますかー?
6÷2(1+2)=9
→6=9×2(1+2)
になるんだけど?
9になりますか? なりますかー?
前者…9
後者…1
ってなった
これの意味が分からない。
あくまでもかっこは中の数を先に計算するというルールだが、
外の数まで先に計算しろというルールなどない。
つまり、かっこの中の計算をした後は外の数を計算し、
最終的にかっこの中の数と外の数を計算するのが正しい計算方法である。
6÷2(1+2)=6÷2(3)
この場合3(3)になって、9になるんじゃないのだろうか。
つまり、かっこの中の計算をした後は外の数を計算し、
最終的にかっこの中の数と外の数を計算するのが正しい計算方法である。×
つまり、かっこの中の計算をした後は外の別の式を計算し、
最終的にかっこの中の数と外の数を計算するのが正しい計算方法である。〇
正しい計算方法とかじゃねえんだよどっちにもとれる問題
1でも9でも正しい
年齢いってるやつは昔学校で習った影響で括弧付属の数字までまとめて計算するから1になる
直前に×があれば9と答える
6÷(1+2)=6÷1(1+2)が間違ってる
だって6÷1(1+2)=6(1+2)じゃんw
というよりは表記の仕方が間違っている。
文字式でないなら×は省略しない。
仮にそれでも省略するのならば÷は使わずに/を使わなければならないし、
その場合は紛らわしさからもう一個括弧が必要になる。
だから
>数学者数名に話を聞いたところ人によって解がことなり、そもそも問題の書き方がおかしいという指摘があった。
って書いてあるんだろ。
式における演算子の優先順位に関する統一機関はありません。
従って、各方面で異なる規則が使われています。
国によっても異なります。
関数電卓の機種によっても異なります。
各種の数式処理システムでも異なります。
さらに数学者によっても異なります。
これらが原因かどうか分りませんが、
学校教育では細かい規則までは指導していないのが現状です。
それでも最近は徐々に一定の規則に収束してきた感があります。
数式処理システムや米国の関数電卓など
①括弧>単項演算子>累乗>単項における乗算>符号>乗除>加減
エクセルなど
②括弧>単項演算子>符号>累乗>単項における乗算>乗除>加減
日本の関数電卓(一部を除く)など
③括弧>単項演算子>累乗>演算子が省略された乗算>符号>乗除>加減
例えば、
-3² は、①なら=-9、②なら=9、となります。
6÷2(1+2) は、①なら=9、③なら=1、となります。
らしいです。
ま、括弧をもう一個つけないと答えが一つに定まらないってことだな。
ニコニコ大百科をみるべし。
ニコニコ大百科でソース付きで論破されていることを、ドヤ顔で主張している。
これは、数学の定義ではないよ
>>1574
理解出来る人は理解出来る人はよね。
沢山の人にとってはその背景を知らないのだと思う。
>>1575
この問題について、ニコニコ大百科などの解釈をめぐるソースはあてにしない方がいい。
理屈を述べ始めたら沢山の人にとって理解不能になるから理屈を述べないだけだと思う。
少なくともこの問題については、答えが9になるれっきとした数学的根拠はある。
むしろ、答えが1になる根拠の方がない。
その数学的根拠を知りたかったら、教師にきいてみるとよい。
人によってはその根拠について知っていると思う。
拒絶反応を起こす可能性が高いだろうから、直接教えるのは控えますが、
分野名について知りたかったら遠慮なく聞いて下さい。
ただ、それを聞いてもそれを理解出来るという保証はないと思います。
歴史の話になるが、これとタイプが似た問題で、
文科省が教えている聖徳太子は実在したか?
というのがあって、どちらかというと歴史学者はその存在を否定しているらしい。
ところが、文科省では聖徳太子が存在すると考えて教科書を作っている。
そして、その教育を受けた日本人の常識では聖徳太子は存在するとなっている。
この計算の問題の答えについての議論は(答えが存在するとしたなら)、
聖徳太子は存在するか否か、という問題についての議論に似ていると思う。
沢山の人は、聖徳太子はいた、と答えるでしょう。
これは、沢山の人が6÷2(1+2)の答えが1、と答えることと似ていると思う。
まあ、最近、文科省も聖徳太子の存在について疑問を持ち始めたらしい。
では、答えがあるとした上で厳密に考えたら、
本来答えは9になることが分かるための学習コースをお教えましょう。
1、大学以降の線型代数と微積分を最初に学習しましょう。
2、次に、集合と位相をしましょう。
3、その後に、群論や環、体(とりわけ、主に群論)について学習しましょう。
そのあたりまで勉強すれば、答えが9になる根拠がよく分かると思います。
むしろ、「÷」を再構成したとき、義務教育のようにはならないことが痛感出来ると思います。
本来は、大学数学で考えたとき「÷」も再構成出来ないといけないんですよ。
では、答えがあるとした上で厳密に考えたら、
本来答えは9になることが分かるための学習コースをお教えましょう。
1、大学以降の線型代数と微積分を最初に学習しましょう。
2、次に、集合と位相をしましょう。
3、その後に、群論や環、体(とりわけ、主に群論)について学習しましょう。
そのあたりまで勉強すれば、答えが9になる根拠がよく分かると思います。
むしろ、「÷」を再構成したとき、義務教育のようにはならないことが痛感出来ると思います。
本来は、大学数学で考えたとき「÷」も再構成出来ないといけないんですよ。
まあ、最初に軽く2、3からはじめて1をして再度2、3を学習するという方法もある
(むしろ、マトモに大学数学を学習するには、その方がいいかも知れない)。
例えば、テキストを挙げれば、
線型代数:岩波講座基礎数学線型空間1、2
(今は非売品だが、ここに既に群論の初歩や環、体の定義程度は載っている)、
微積分:同講座解析入門1~4か、杉浦先生の解析入門など(どちらも位相の初歩は必要)、
集合と位相;現代数学概説Ⅰ、Ⅱの該当する部分(これらは基本なので丁寧に読んだ方がよい)
群論、環、体:岩波講座基礎数学の該当する書籍
(環と加群は、全体的にだがとりわけ多項式の定義の部分が丁寧で分かり易い)。
>>1586の類のテキストを或る程度、例えば群論(群作用含む)の初歩あたりまで読み進めれば、
答えが9となる根拠がよく分かると思います。
群、環、体、線型代数、位相についてなら、現代数学概説Ⅰ、Ⅱにも或る程度は載っています。
これで事足りるような気がしないでもありません。
ただ、ε-δ論法はまだしも、リーマン積分の計算などの普通にいうような微積分の基本は余り載っていません。
まあ(かなりハードになるかも知れないが…)、>>1586で挙げたテキストより読み易いかどうかはともかく、
ガロアの夢(内容はともかく書き方は、今でいうマンガで分かるシリーズに近い)を軸にして、
そこに参考書として挙げられたポントリャーギンの連続群論上下
(書き方はともかく、どちらかというと上巻の方は読み易いと思います)
などを読んで行くという方法もある。
そこにはシュヴァレーのリー群論や解析概論、松島先生の多様体入門など、
名著が多く参考書で挙げられている。勿論、ガロアの夢自体も名著。
これらが読めれば、嫌でも群論「だけ」についてはかなり分かると思います
(むしろ、集合と位相程度は前提になっている)。
あと、アドバイスすると、>>1586や>>1588の書籍を読むにあたり、
高校までの数学を1通り全部学習しておけば、受験数学に特化するまでになる必要はないぞ。
高校までの数学に慣れておく程度で十分。
ただ、一応(大学以降の)物理も学習した方がよいかな。
むしろ、論理的な記述力や読解力(いわゆる国語)をしっかり見につけた方がよい。
>>1478で書いたとおり、答えは式の書き方がおかしいだよ。
一々「6÷2√3」を「6÷(2√3)」などと書くことも大変でしょう。
そういうことが出来るなら話は別だけど。
多分それが出来ないから「a÷bc=a÷(bc)」みたいな式を用いて教育をしているんだろう。
まあ、答えがあるなら、本来数学的にはそれは9になる。
時間的事情や社会的事情などのいわゆる空気を読んで考えると、答えは1にもなる。
ただ、答えが1になる数学的な根拠はないに等しい。
式は合ってるの?間違ってるの?
「6÷2√3」などの他の式とは違い、
「6÷2(1+2)」は非常に誤解を招き易い形で
共通の言語の数学としての役割を果たさないから、
単純に式が合っているか間違いかの2択でしいて答えれば、間違い。
そもそも、この式が「6÷2√3」などの他の式と同様に式自体が合っているなら、
答えを巡る論争なんて起きないでしょう。
「6÷2(1+2)」は、単純に答えを1として済む式ではない。
義務教育でするような多項式の計算をするのかが聞きたいよ。
普通に考えれば、「2×(1+2)=2×3=6」と考えて計算するでしょう。
誤解を招かぬように書くと、>>1593、>>1594は
>>1591で書いたような、時間的事情や社会的事情などの
空気を読んで考えて義務教育に合わせたときの話ね。
仮に毎度毎度丁寧に「6÷2√3」を「6÷(2√3)」と書いて
「6÷2√3」と「6÷(2√3)」を異なる式として区別して扱っているようなら、
「6÷2(1+2)」はそれ自身は意味を持つようになる(いわゆる群論の考え方)。
本来は「6÷2(1+2)」は、それ自身で意味を持つ式にならないといけない筈なんだけど、
時間的社会的事情により共通言語の数式になっていないという、不思議な現象が起きている。
>「6÷2(1+2)」はそれ自身は意味を持つようになる(いわゆる群論の考え方)。
は
>「6÷2(1+2)」はそれ自身「で」意味を持つようになる(いわゆる群論の考え方)。
の間違い。
私の解答は、1または、9の2とうりあるので、解がひとつに決まらない。式が悪いとか答えるけど、あなたの回答を教えてください。
そういう人は、どうこたえたらいいの?覚えるしかないと思うんだけど
A 最低でも、大学の数学科以上でないと、わかりません。私のわかる範囲では、①2とうりの解釈があるので、問題不備。②省略された積を復活させて、9 ③0次式と見て、1
②と③はうまく説明できる自信がないので①にしておくと答えると思いますが、このこたえはあってるのですか?間違ってるのですか?
逆に、うまく説明できたら、②も③も解答としてはアリなのですか?なしなのですか?(②の根拠は散々説明してくれましたが、解答としてどう書けばいいかわからない)
(続き)
そもそも、高校までの数学は論理的に曖昧な部分があるのに、
他国の義務教育の問題を自国の義務教育の基準に
照らし合わせて考えること自体がおかしいんだよ。
自国は自国で基準を作り、その基準に照らし合わせて義務教育を行う。
時代により教える内容も異なってくる。日本でもそうでしょ。
日本の教員免許が外国では通用しなくなる。国語の教師なんてその例でしょ。
外国の教員になるには免許を取り直す必要がある。数学もそうだろうよ。
だから、電卓でもどこの国で作られたかで答えが違ってくるんだろうよ。
他国の義務教育の問題を考えるなら、普遍性のある方法を取った方がよい。
紛れの虞が無いならば g • x などの演算を省略して gx のようにしばしば略記する。
紛れがあるんだけど、その場合はどうなるの?
>>1598
>>1605の補足をすると、そこで書いたように、他国の義務教育の問題とその答えを
自国の義務教育の基準に照らし合わせて考えて
「正しい答えは1であり9にはならない」などと考えることは意味がない。
他国にはその国の基準がある可能性が高い。
無理矢理自国の基準に照らし合わせて答えは1と考え他国の答え9が間違いと考えても意味がない。
最終的には、その基準さえ見つかれば、1でも9でもいいってことになるんだけど。数学って、基準探し?
既に基準がしっかりあるなら、電卓の答えが
どこの国で作られたかで答えが違うなんてことはあり得ないだろうよ。
高校までの教育には、他国にはその国の基準があると思うよ。
群論はれっきとした世界共通言語の数学になっているから。
各国で定めた高校までの数学とは違い、(理学部)数学科以上でするような数学の内容が、
国の基準や時代の変化で内容が覆るなどということはあり得ない。
高校までの数学は、論理的に曖昧で国の基準で違いが生じ得るから、曖昧以外の何物でもない。
台湾人が日本で書いたら、その人のルールで計算し、日本人とは答えが違ってくるだろう。
それこそ今までいわなかったけど、数学以前に国語をしっかり身につけてほしい。
同じ人かどうかは知らないが、「とうり」は正しくは「とおり」だよ。
それこそ、これは国語で習ったようなことではないか?
余りに国語が出来ないと、論理的思考をすることは出来ないと思われる。
国語が出来ないと、論理的な文章の読解や論理的な文章の表現もおぼつかない。
一応いえば、有限性を伴う代数的な式は群論で扱える。
義務教育に出て来る程度の多くの式は、
すべて有限和だったり有限積だったりして代数的な式で有限性を伴う。
そういう問題が生じるから、問題の書き方がおかしいが妥当だっていったでしょう。
役人が検定した教科書の内容だけが数学だと考えたら大間違い。
役人には群論などの大学以降の数学を知らない人が多い。
役人にキレてお茶をぶっかけたような人がいる位だ。
違っていれば訂正すればいいだけのこと。それがないなら教科書が正しい。
キレてお茶をぶっかけるとか、どこのキチガイだよ。数学を語る資格はない
誤解はないとは思いますが、>>1622は日本の基準での話ですよ。
>>1622
>>1623の
>役人にキレてお茶をぶっかけたような人がいることは
は
>役人にキレてお茶をぶっかけたことは
と訂正します。こういうサイトがかなりあるので、多分事実でしょうね。
溝畑宏氏は父から、官僚になるなら板前になったらどうだ、といわれたらしいですしね。
>>1624では>>1622ではなく>>1623ですね。
>>1623で書いた内容は日本の基準に合わせて考えたときの話です。
幾度も間違えてすみません。
9が間違いなのは現時点での数学では明らか。
そうしたら数学自体を否定しだした・・
何も変なことではない。
9が間違いで1が正しいことが明らかな訳でもない。
むしろ、>>1604で書いたように、答えがあるとするのなら、9とする方に論理的根拠がある。
そもそも、誰がどのような場面で「2×(1+2)=2(1+2)」と紙に書いて計算するのか、
と聞きたい。普通の感覚では「2×(1+2)=2×3=6」と考える筈。
簡単にいえば、世界共通言語としての数学では、
日本の役人が決める数学の基準が絶対的とはいえない。
もし絶対的であるのなら、既にその基準が世界共通になっていて「6÷2(1+2)」の解釈をめぐる論争は起きない筈。
ふつうに、文字式学んだら、×(ばつ)は、x(エックス)と間違えやすいので、省略して書いたほうが、計算ミスが減ると教えられましたが。
サイト見た?官僚の態度が悪かったようですよ。
>>1630
私はそんなことを聞いた記憶はないです。
×(掛ける)と小文字のxは大きさが違い、小文字のxを筆記体で書けば×(掛ける)と間違えることはないと思いますね。
>>1623で挙げたサイトのことですよ。
簡単にいえば、加減乗除の計算するとき「÷」という記号は出来るだけ使わない方がいいんです。
一応、余計なことかも知れないですが、今後のためを思い日本語の間違いを指摘します。
「思いどうり」ではなく正しくは「思いどおり(通り)」です。
この種の間違いをすることは、した人自身の日本語力がかなり悪いことを示しているようです。
それ程よくない間違えのようです。
サイト見ましたが、態度が悪いからお茶をかけたしか書いてません。それを美談にしてることがわかりません。であれば、お茶かけといて自分は正しいとか。唯一否定できるのは、思いどおりかな。で、お茶かけた人は、6÷2(1+2)にいったい何の影響ある話なの?
>>1623への回答のため用意したに過ぎません。
「6÷2(1+2)」とは関係ないと思います。
美談に見えるかどうかは個々人で違い、主観的な問題です。
ただ、推測に過ぎないですが、高校の教科書作成者であった可能性はあります。
「>>1623への回答」ではなく「>>1622への回答」だったな。
まあ、人間として、官僚の態度が悪かったらキレることはあるでしょうね。
態度の悪さの度合いにもよりますけど。
群論で計算する方法と括弧()をΣと見なして計算する方法について。
どちらが簡単かは微妙だ。微妙過ぎて私には分からない。
どちらが数学的な書き方として理にかなっているかというと、群論を用いた方だ。
括弧()をΣと見て計算する方法は「6÷2Σ」の形の式を計算することになる。
普通は「6÷2Σ」とは書かないな。群論では「÷」を再定義すれば
「6÷2(1+2)」と書くことは十分可能で「2(1+2)」の形の式は普通に出て来る。
そういう訳で、群論で答えを9とした方が妥当でしょうとして答えがあるならそれを9としている。
そうすれば、小学で定義する「÷」と中学で定義する「÷」にも一貫性が出て来る。
私は既に問題の書き方がおかしいと指摘したのに、
まだ答えがあると思って議論しているのはどういうことかとね。
高校の予備校講師には、中には群論とかを知っている人がいるとは思うぞ。
余談だが、東大や京大の大学受験だと、指導要領外の数学も使っていいらしい。
そういうこともあり、教科書の内容だけが数学ではないんだよ。
教科書に沿って考えさせることは、
学問としての数学の精神に反するという考え方をしているらしい。
>>1640の括弧()をΣと見なしたときの計算方法は
>6÷2(1+2)=6÷(2×1+2×2)=6÷(2+4)=6÷6=1
になるだろうな。
>6÷2(1+2)=6÷(2(1+2))=6÷(2×3)=6÷6=1
だとΣの部分「1+2」を有限和の値と見なしたことになり、
これなら群論で考えてもよくなる。
群論の計算方法と括弧()をΣと見なしたときの計算方法のどちらが簡単かといえば、微妙だ。
東大とかが出す問題は、確かに教科書とは違うだろうが、
教科書の内容を理解してなかったらまず解けないだろ?
教科書だけが数学ではない?よくわかんないけど教科書に
反する解き方をするのは間違いなんじゃないですか?
指導要領外の数学と教科書のルールに反する数学もどきは違います
この計算に対してfacebookでは342万人が解答し正解者(不正解者?)は149万人だったという。
どの面でこんなこといったんでしょう。この教師。
自分で高校までの数学から出発して定義していって使うなら、
偏微分とか群論とか大学以降の数学も使ってよいらしいよ。
そういうサイトがある。
論理的に合っていればそれでよいという考え方をするようだ。
ただ、その分、採点基準は厳しくなるらしい。
>>1648
大学以降の数学も立派な数学。
高校までの教科書内容だけが数学であるのなら、
人によって年代によって数学の内容が異なることになる。
私=>>1584~1591は教師でも予備校講師でもないぞ~い。
群論とか等位の考え方という言葉を持ち出したりはしたが。
>>1652の話で、f(x、y、z)=x、g(x、y、z)=yz、と定義すれば
a÷bc=f(a、b、c)÷g(a、b、c)=a÷(bc)
となって「a÷bc」は「a÷(bc)」を指すことになり、
f(x、y、z)=x、g(x、y、z)=y、h(x、y、z)=z、と定義すれば
a÷bc=f(a、b、c)÷g(a、b、c)h(a、b、c)=f(a、b、c)÷g(a、b、c)×h(a、b、c)=a÷b×c=(a÷b)c
となって「a÷bc」は「(a÷b)c」を指すことにもなる。「a÷bc」の解釈次第だ。
こういう話まですると、普通の群論なのかどうか分からないけど。
それより、
>現代数学の「間違いっている」解き方を合ってるとして計算ということですね。
は
>現代数学の「間違っている」解き方を合ってるとして計算ということですね。
という意味でよろしいか?
どうしたら「間違いっている」という発音(「まちがいいっている」とでも発音しているのか?)
なのか表現なのか分からないが、そういうことが出来るんだ?
本当に数学以前に日本語をしっかりさせた方がいい。余りにも日本語が酷過ぎる。
数学より国語(日本語)を勉強した方がよいのではないか?
数学以前に、日本語をしっかりさせましょう。
瑣末なことだが、>>1657の「という意味でよろしいか?」は「と書いたつもりか?」の意味で書いた。
何れにしろ、
>現代数学の「間違いっている」解き方を合ってるとして計算ということですね。
という文では、「間違いっている(まちがいいっている?)」は、
「間違っている(まちがっている)」か「間違い(まちがい)になっている」かなど、
何かに訂正しないと、日本語として意味が通じない。
或いは紙に文章を書かなくなった影響なのか。
読書不足や紙に文章を書かなくなったという類のはよく聞く。
まあ、もうここに書くことはやめる。
ここまで日本語の表記が酷い人(日本人ですよね?)を見たのも、はじめてです。
とうり(通り)という日本語の表記が定着していることも、ここで知った。
何かソースを頼む
>読書不足や紙に文章を書かなくなったという類のはよく聞く。
という部分を
>読書不足や紙に文章を書かなくなったという類の「話」はよく聞く。
と訂正させてもらいます。
残念な人だった。
小中学生でもわかることを必死に否定して、少し頭がおかしいのかもしれない。
きっと日本人じゃないから海外では・・とか言ってたんだろうな。
もう出てくるなよ。
自分で群論を勉強しましょうとしかアドバイスしようがありません。
群論の初歩や線型代数、微積分などを身に付けることが先です。
群論を全く知らないといわゆる等位の考え方を理解することは難しいと思います。
学習するための順序は>>1584に書きました。
テキストは必ずしも>>1586などで挙げた書籍を読む必要はありません。
ただ、信頼出来るような書籍を挙げたつもりです。
例えば、岩波講座基礎数学の線型空間1、2では差分方程式や微分方程式の解法を扱っていたりもするので、
普通の線型代数のテキストとは違うとは思います。
その1巻目にも群論や環、体の基本は書いてあります。
例えば、「とうり」などという表記はタイプミスの類ではなく、
それ以前の致命的な日本語力の欠如を指し示すものだ。
それ程日本語が乱れているということだ。
私は日本人だ。
ここの沢山の人達が群論を知らない。
それに尽きると思う。
例として、カラスは黒いの話しようか。一匹白いのが見つかっただけで、その根拠は覆るはずだが、今回の場合、300万人中約半数反論が見つかった。では、その定義は本当に正しいのってことになる。あくまで、群論という考えかたがあるという程度だと思う。その群論だって、定義いじれば、成立するんだよね。もうひとつ、今回は、解答の根拠を群論とおっしゃいますが、そもそも、出題者の出題ミスならどうなる?そうだとしたら、議論は、群論じゃないってことになるけど。式は正しくないといいながら、正しいといっているのが気になったので。
物理学者が学ぶ、日本国の数学と、化学者が学ぶ、日本国の数学と、高校の普通科で学ぶ数学と、群論と…。このやり方なら、1か9か無数に計算の定義できますよね。それを、群論は絶対だ。だから、みんな間違いだ、群論学んで再定義しろとやっちゃうと、群論以外は全て書き直になる。そこまでは暴論だと思います。でも、あなたの言い分は、それしかない言い方をしている。そこが引っかかります。
その式が出題ミスだったなら、台湾国内の問題になるだろうが、台湾で答えを9としているところを見ると、
日本国内では出題ミスとなるが、台湾で出題ミスになっているとは思えない。
>>1674のような事情もあり、私は既に式の書き方がおかしいと指摘している。
まあ、群論を知っている立場から個人的主観的見解をいわせて頂けば、
「6÷2(1+2)」の答えがあるなら、本来は9であるべきですよ。答えを1とする立場は
括弧内の「1+2」を有限級数と考えて「6÷2Σ」の形の式を書いたり、
括弧()を含めた「(1+2)」の部分を1次の正方行列と考えて「6÷2[1+2]」と書くような立場に近いんです。
普通、1次の正方行列というのは考えません。
ちなみに、物理や時によっては化け学でも群論は用いているようです。
一応、群論を知っている人が群論を用いて「6÷2(1+2)」を計算すれば、
物理学者や化け学者でも答えは1になります。
いつどこで誰がしたかなどの、時期や場所、それをした人によって、
群論による計算の答えが変わることはあり得ません。
問題は、「6÷2(1+2)」の答えがあるなら、
置き換えで計算することと群論で計算すること
の、どちらがよいかだと思います。
これを置き換えで計算する方法を取ると、便利な方法ですが、小中での割算に食い違いが生じています。
群論で考えたとき、置き換えは「a÷bc=a÷(bc)」という公式を認めることと同じ方法になります。
群論の計算だと、論理的な方法ですが、他の割算を計算するときなど、面倒な表記になることがあります。
>物理学者や化け学者でも答えは1になります。
の「答え1」は「答え9」の間違いでした。
すみません。
>の「答えは1」は「答えは9」です。
の部分は
>「答えは1」は「答えは9」です。
です。すみません。
>>1676では、正しくは
>物理学者や化け学者でも「答えは9」になります。
です。
答えがあるなら、そういう問題です。
公式を使うのではなく置き換えて計算すれば、
論理的には置き換えでも群論でも、どちらでもよいです。
ただ、個人的には、「6÷2(1+2)」という式は、
代数的な式と見て群論で答えを9にする方が、
数学の感覚としてはよいと思います。
普通は「6÷2Σ」や「6÷2[1+2]」のような式は書きません。
大事なことを書き忘れましたが、論理的な飛躍や曖昧さ、表記の違いが生じていても、
論理的に厳密に考え直したときに結論が今までの結論に一致しているようであれば、
物理学科や化け学、工学部で学ぶ、ラプラス変換やベクトル解析などの、
いわゆる応用数学や高校までの数学も、普通の数学の一部であると考えています。
論理的な厳密さや表記法は人により異なります。
ただ、「÷」がある割算を計算するときはともかく、
それを厳密に再構成するとなると、やはり群論で再構成することになるでしょうね。
置き換えはどちらかというと解析的な計算をするときに多く使いますので。
果たして置き換えによる厳密な再定義が出来るのかどうかは分かりませんが、
群論での考え方は「a÷bc=a÷bc=a÷b×c」であり、「a÷bc≠a÷(bc)=a÷(b×c)」です。
元々、高校以降では「÷」の割算の厳密な或いはマトモな定義という代物を聞いた記憶がありません。
また、高校のとき使った参考書を見てみましたが、「÷」について細かくは書いてありません。
群論での「÷」の割算の再構成は自身でしてみました。
>置き換えはどちらかというと解析的な計算をするときに多く使いますので。
の部分の一部を、
>置き換えはどちらかというと解析的な計算をするときに多く「します」ので。
と訂正します。
>「÷」がある割算の再構成
の「再構成」は、「再定義」として
>「÷」がある割算の再定義
などと「再構成」を「再定義」に直して読んで下さい。
自分から見れば「再構成」ですが客観的には「再定義」で、微妙に意味が異なる気がしますので。
まあ、もうここに書くことはやめる。
責任は持ちましょう。書きたいなら撤回しなさい。
何回書いてるんだか。人を批判する以前に自分が一番愚かだと知りなさい。
あと不特定多数の人が見る掲示板で専門用語を偉そうに並べるのは無能な
証拠です。分かり易く説明するのが常識です。ここは学会ではありませんよ。
>>1475や>>1478あたりで要点は既に分かり易く説明したよ。
分野名は出したけど、専門用語は余り使っていない。
せいぜいラプラス変換とか有限和とか有限積、有限級数、差分方程式、微分方程式、群、環、体、群作用位かな。
それでも、ラプラス変換とか微分方程式を知っている人は多い。
特別難しい専門用語は用いていない筈。
あと、普通の人にとって鬼畜に感じるテキスト(中身は文句ないと思うのだが)を挙げたりはした。
私がしたことは人の批判ではなく、悪い日本語の訂正ですよ。
日本語の能力がないというような類のことは書いた。
能力がないと指摘することは人の批判とは少し意味合いが違いますよ。
人の批判なんていったら、人格批判なども含まれます。
「通り」を「とおり」ではなく「とうり」ということは、
「2通り」などというように「通り」を単位として用いたときに
「2通り」を「2とうり」と書いて正しいとしているということ。細かくいったらこういう書き方はしないよ。
私が訂正しなかったら誰が訂正したのだろうか、と。
むしろ、自分の日本語に厳しくしない人が他人の日本語を訂正する資格などないと思いますね。
>まあ、もうここに書くことはやめる。
と書いたにもかかわらず、それ以降も書いているから論理的におかしいという理屈は、
常識では通用しても、本当の意味で、論理的には通用しません。
常識的に考えたときにおかしいと批判することは、AさんとBさんがいて、
A:「前に何々だといったではないか」
B:「確かにそうだったな。悪い」
なら通用するけど、
A:「前に何々だといったではないか」
B:「そうだったけ?忘れたな」→2人の間で争いが起こり得る
だと、全く通用しない理屈ですよ。後者のような話はよくあるでしょう。つまらないツッコミに過ぎません。
続き)→(続き)
と訂正。
>つまらないツッコミに過ぎません。
を
>中身的にはどうでもいいツッコミに過ぎません。
と訂正。
私は国語(日本語)が専門ではないから、そこまで厳しく指摘はしないけど。
それでも、或る程度は厳しく自分の文章を厳しく書いているつもりなんだけどね。
群は掛け算と割り算が自由に出来る数の集まり、
環は足し算、引き算、掛け算が自由に出来る数の集まり、
体は足し算、引き算、掛け算、割り算が自由に出来る数の集まり。
×、÷、省略された×の演算順序は、群、環、体では同じと考える。
他の計算の優先順位は普通の考え方と同じ。勿論0で割ってはいけない。
>>1685
幾らなんでも、群、環、体を見てそれを専門用語といって私を無能だというようでは困る。
ごくごく普通に最初に基本の部分で出て来る。
「集合」を「集まり」より分かり易く説明することは不可能に近い。殆ど日常用語と同じ意味だよ。
数学に限らず、普通に「集合」を「集まり」の意味で使うでしょう。
基本的に、>>1685みたいに人を無能呼ばわりし出す人が無能なんだよ。
私を無能呼ばわりする暇があるなら、9になる考え方を分かり易く説明してみてくれよ。
私のようなことを自身で何もしていないのによく他人を無用呼ばわり出来るね、っていいたいよ。
(一旦終了)
>私のようなことを自身で何もしていないのによく他人を無用呼ばわり出来るね、っていいたいよ。
は、
>私のようなことを自身で何もしていないのによく他人を無「能」呼ばわり出来るね、っていいたいよ。
と訂正。
になったんだけどw
>まあ、もうここに書くことはやめる。
と書いたにもかかわらず、それ以降も書いているから論理的におかしいという理屈は、
常識では通用しても、本当の意味で、論理的には通用しません。
=常識が通じないってことでOK?
答えがあるなら、それでもよい。
ただ、>>1675で書いたように、数学の感覚は悪い。
少なくとも「6÷2(1+2)」の場合、何にも問題なく答えを1にする方法は、
「6÷2(1+2)を計算せよ」なんていう出題ではなく、
「t=2(1+2)のとき、6÷tを求めなさい。」みたいな出題の仕方だよ。
それなら、群論で考えても
6÷t=6÷(2(1+2))=6÷(2×3)=6÷6=1
になって、答えは1に一致する。決定的な問題は生じていない。
「6÷2(1+2)を計算せよ」なんていう書き方だと、書き方が曖昧で答えがあるなら9にもなる。
数学は自然科学に限らず社会科学でも現象を述べる言語として用いられていて
それ自体が表記法や用語などの見てくれは時代で変わることがあっても、
それらが表す中身としての本質的内容が変わることはあり得ないような普遍の言語だから、
数学を語るにあたり常識は関係ない。
常識を持ち出して考えたら、場所によって人によって数学の本質的内容が異なることになる。
個人的意見に過ぎないが、数学の感覚は大事だとは思う。
まあ、歴史的には曖昧に用いていた数学の正しさが後から裏付けされていくということが多い。
中には必ずしもその解釈が正しいとは限らず、後で別の解釈があったということが分かって
その別の解釈に基づいた数学が発展していくこともある。
勿論、今までの解釈の内容が正しいとした上での話。
例えば、中学で習う2本の平行な直線は交わりません、というのがその1つ。
本当は、2本の平行な直線は2点で交わります、などとしてもよい。
ごめんね。交わるときもあるんだ。球面上に平行な線引くと交わるんだ。何でこんなこと考えるかというと、全てのものが平面状で考えられればいいんだけど、例えば、地球上の光の軌道とか考えるのに(例えば、太陽の日射とか、GPSとかね)そういう学問もあるんだ。逆に、球面で考える場合、地球に平行に入ってきた光が交わったりすると考えると、すっきり考えられたり。ただ、これが「6÷2(1+2)を計算せよ」にどう関係あるかがわからないけど。あ、ちなみに、2本の平行な直線は交わりませんって言うのは正解で、球面で考えるほうが、普通イレギュラーだから、堂々と交わらないといってください。
群論→3x÷3x=x^2
自分が中学、高校生なら、1とこたえます。だって、間違えたくないから。点数関係ないのなら、どちらでもいいです。あいまいにしか定義されていないかもしれませんが、点数にはしっかり反映されますが。
そもそも球面上でも交わらないんじゃ・・
交わった時点で平行線が交わるというより、そもそも平行じゃなかった!
が正しいんじゃないか?頭が固い私にはワカラン
>>1703
そこまで撤回を求めるなら、>>1661は撤回する。
北極から南極に、出来るだけその間の距離を近くさせるように、2本の直線を引いてごらん。
すると、その2本の直線を赤道のあたりで見ると観測者には平行に見える。そして2本の直線は南極で交わる。
2本の平行な直線は交わりません、というのはそういうこと。
こんなこといい出すと、数学の内容が多数決で決まることになるよ。文脈から、
>群論で考えるのは常識です!教科書は、特殊な考えなので否定してください。
って
>群論で考えるのは「非」常識です!(群論の)教科書は、特殊な考えなので否定してください。
だよね?
「÷」を群論で再定義すれば群論で考えることも出来るんだから、ただポンと
「6÷2(1+2)を計算しなさい」と出題されると9にも出来る。
「6÷2(1+2)を計算しなさい」に答えがあるなら、それは場面で異なる。
かまわないんじゃない。「6÷2(1+2)を計算しなさい」の答えなんて、最終的にはそれでいいのかもしれません。
球の上下に直線を数本結ぶとどれも平行にならないですよね?
そもそも球状に直線と言うのが無理な話なのでは?
ただ天に向かって2本の直線を伸ばせば永久に交わらないのかな。それが本来の平行なのかな?
それでも自転公転、その他要因などの影響で交わってしまうということ?きりがないな。
平行とは言わないのでは・・
多数決で決まることになる。それでいいと思います。
そもそも初期は1,9派ほぼ同数だったのに今では9と言う人ははめっきり少なくなりました。
それはいろいろな矛盾や公式などを指摘され、9は間違いと思う人が増えたからです。
絶対の自信やソースがあれば堂々と振りかざせばいいだけですが、それがない。
出てくるソースは皆無。矛盾を指摘されても答えられず。
それらを論破できないからここまで小さくなったのです。
>>1717の「なんて」という言葉を持ち出している点から推察すると、多分、理由は
>それはいろいろな矛盾や公式などを指摘され、9は間違いと思う人が増えたから
ではなく、「6÷2(1+2)」の答えがあるとしてそれを求めることに、
数学的な意味合いは何もないと考えているからだよ。
数学的には球面などの話の方が面白いんだよ。
意味があるとすれば、電卓など数学ではない世界の話になる。
数学をするにあたり根拠を挙げるのにソースなんていらない。
自分の頭で考えるだけ。数学は文献を出しまくるものではないんだよ。
基準を決めてなければそもそも答えだすのは不可能。
6÷2先にするのか、2(1+2)を一つの数としてみるのか決めて欲しい。
平行の定義は直線(平面)に対して垂直な2つの直線(平面)であった気がします。
そもそも地球を球体としてみれば分かるが北極~南極を(地球上を通り)直線で結ぶのは不可能では?
結局、曲線になりませんか?平行の捉え方を間違ってると思います。
本来は曲線というべきだが、分からないっていう人がいたもので、
厳密さをかなり損ねて分かり易く書いたつもり。直線はそのための表現に用いた。
地球上に引いた2本の曲線の接線を引くと平行になるとき(赤道上)があるが、
2本の曲線自体を赤道付近で観測したらどうなるか、といったら、
観測者には、平行でない2本の曲線があたかも平面上に引いた2本の平行な直線に見えるでしょう。
>>1712ではそういうことをまとめて書いた。
まあ、赤道上の観測者から見たら、正確には遠くの1点に向かっているような
2本の直線(沢山の人が定規で直線を引くとかいう意味でのね)っていう感じになるかな。
観測者にとって2本の曲線は、画家が描いた絵の直線のように見える。
「6÷2(1+2)」に答えがあるなら、やはり本来は群論のように「6÷2」が先でしょうね。
例えば、「6÷2(1+√2)x」のときは割る数をt=2(1+√2)xとおいても、tはこれ以上計算出来ないです。
このときは「6÷2(1+√2)x」は「6÷t」になります。何も誤解などの特別な問題はないと思います。
「6÷2(1+2)」だと、割る数をt=2(1+2)とおくと、tは「定数項いわゆる数として」まだ計算出来る状態です。
このときも「6÷2(1+2)」は「6÷t」になります。
割る数を置き換えたとき、「定数項いわゆる数として」まだ(文字を含まない式として)計算出来るかどうか。
「6÷2(1+2)」については、このあたりが普通の割算と違うと思います。
(>>1730の補足)
同じ割る数を置き換えたときにそれを「定数項いわゆる数として」まだ計算出来る状態の式でも、
「6÷2^3」とかなら多分何も誤解などの特別な問題はないと思います
(私でもこういう式については、「2(1+2)」とは違い、「2^3」をすぐに群論で考えて計算するとは限らない)けど、
やはり「6÷2(1+2)」だと、簡単に群論で考えて計算出来ます。
そのあたりですね。「2(1+2)」は群論でごくごく普通に出てきます。
群論は分からないけど、以前もめてた時にa÷bc=a÷b×cだと言ってましたよね。
さすがにそれが違うのは自分でも分かります。6÷2kは3kにはならないですよね?
どこが違うんですか?自分的には1722さんの方が納得できます。
この考え方をしないとテストで不正解連発するのが実際にやってみれば分かると思うが・・・私の記憶が間違っているのか
勘違いしないで欲しいけど、ニコニコが言ってるのではなく、各方面のソースがまとめてある。
それを9派、不備派はバカにする傾向があるけど、具体的な反論はない。
ニコニコとか何だよww!とかニコニコ信者とか。そんなもの。
あるとすれば、1という答えに反論はできないけど、こう考えれば9じゃん!とか、
文字じゃなきゃ×は省略できないから式が間違いとか。(それでも1という根拠も載ってる)
逆に9、不備とする人に、ソースはないの?と聞くと、だんまり。自分の意見を言うだけ。
そして論破され終了。で、しばらく消えて時が経ってまた9だ不備だと言い出す。
ソースの中身に具体的に反論しない(できない)でしょ?
そんなもんだ。なぜ9、不備のソースがないのかよく考えた方がいい。
分かってるじゃん、9、不備にはその基準すらないんだよ。
私は答え1になる基準で解いた。9だなんて言っていない。思い込みである。
私は答え9になる基準で解いた。9だなんて言っていない。思い込みである。
私は答え9になる基準で解いた。1だなんて言っていない。思い込みである。
数学においてソースや権威のある人の名前で固めた定義、公理、定理
例えば、ピタゴラスの定理とか、オイラーの定理とか、一般に認知されていて、どこからも反論の来ないようなら、かまわないと思いますが、教育委員会のだれそれとか、静岡県教授のだれそれとか。そういう意味です。
数学においてソースや権威のある人の名前で固めた定義、公理、定理なんか聞いたことありません。
数学においてソースや権威のある人の名前で固めた定義、公理、定理で、例えば、ピタゴラスの定理とか、オイラーの定理とか、一般に認知されていて、どこからも反論の来ないようなら、かまわないと思いますが、教育委員会のだれそれとか、静岡県教授のだれそれとかそういう人で固めた数学の定義、公理、定理は肯定できるかといったら、難しいと思います。(同じ理由で、否定も難しいが)
に訂正します。すみません
ら、思った以上に続いてたんで記念カキコ
あちらはあちらを補足します。
>>1746において、教育委員会のだれそれとか、静岡県教授のだれそれとかそういう人で固めた数学の定義、公理、定理は肯定できるかといったら、難しいと思います。(同じ理由で、否定も難しいが)
この部分で、肯定、否定の判断が、数学的にどうかということの検証(特に、否定の部分ね)がどちらかわかりかねるので、ニコニコの結論も、議論の末そう決まったのなら、それでいいという意味です。こっちで、ニコニコの議論したわけでもないし。逆にこちらは、ルールとかソースとかに縛られてないので、思い思いに書いてくれればいいと思います。後、ニコニコの議論は、ニコニコでやってね。でないと、もうむちゃくちゃになるから。
これは歴史じゃねーんだから、権威なんか求めんなよw
これは数学だぞバカヤロー。
数学にソースなんか一切不要。数学で重要なのは、ロジック。「ロジックがすべて」。ロジックが正しければ、すべて正解。
逆に、フィールズ賞受賞学者の意見であっても、「ロジックが誤って」いれば、全て不正解!
数学に権威なんて関係ねーんだよ、重要なのはロジック。
それくらいわかっとけ!
文系乙ww
で、具体的なソースの中身に対する反論は?
ソースの中身のロジックがロジックが誤っているのはどの部分?
それぐらい書けよ。中身も見ないでソース自体を批判?
バカじゃねーの、クソニートが
だから「a÷bc=a÷bc=a÷b×c」であり、「a÷bc≠a÷(bc)=a÷(b×c)」
これをなぜ公式と違うのかを説明しろって言ってるのになぜスルー?
あとニコニコ内のソースを使ってはいけないのはなぜ?ここはニコニコではないが
ニコニコでまとめられたソースを言ってはいけないわけ?思い思いに書けばいいんじゃないの?
都合の悪いことは書かないで、ってこと?なぜむちゃくちゃになるのか分かれよ。
で、具体的なソースの中身に対する反論は?
ソースの中身のロジックがロジックが誤っているのはどの部分?
それぐらい書けよ。中身も見ないでソース自体を批判?
バカじゃねーの、クソニートが
1750では上記のことには触れていませんので答えなくてもよろしいかと
またニートとも限りませんね
だから「a÷bc=a÷bc=a÷b×c」であり、「a÷bc≠a÷(bc)=a÷(b×c)」
これをなぜ公式と違うのかを説明しろって言ってるのになぜスルー?
上記については1749に質問していないからでは?
あとニコニコ内のソースを使ってはいけないのはなぜ?ここはニコニコではないが
ニコニコでまとめられたソースを言ってはいけないわけ?思い思いに書けばいいんじゃないの?
都合の悪いことは書かないで、ってこと?
上記については1749はこのことは何も記してませんね
ソースを言ってはいけないというルールはないと思うので、言っていいと思います
むちゃくちゃは意味がよく分かりません
簡単にいえば、式「6÷2(1+2)」について「2(1+2)」を積と考えるところは
答えがあるなら、それを1とする立場でも群論で9とする立場でも同じです。
「2(1+2)」を積と考えることは、「2(1+2)」を
数としての「+2」と同じく数としての「+3」との積と考えることと同じです。
これは
2(1+2)=2(+1+2)=(+2)(+1+2)=(+2)(+3)
という式が成り立つことから分かります。
で、「6÷2(1+2)」を6を+2と+3の積「(+2)(+3)」で割った式として書きかえると「6÷(+2)(+3)」となります。
「6÷2(1+2)」という式は、見た目は違って見えても中身としては「6÷(+2)(+3)」という式と同じなんです。
群論で答えを9とする立場は、
6÷(+2)(+3)=(+6)÷(+2)(+3)=(+6)÷(+2)×(+3)=…=9
として考える立場です。
群論では「6÷(+2)(+3)=6÷2(1+2)」と「6÷((+2)(+3))=6÷(2(1+2))」とを区別します。
「6÷((+2)(+3))」だと群論でも
6÷((+2)(+3))=(+6)÷((+2)(+3))=(+6)÷((+2)×(+3))=(+6)÷(+6)=1
になります。答えを1とする立場は、後者の計算をしている訳です。
群論では「6÷(+2)(+3)≠6÷((+2)(+3))」とします。違いはそのあたりです。
ついでに、幾らソース云々を挙げたところで、群論の考え方(答えがあるなら9)を否定することは無理でしょうね。
高校までの数学のような論理で群論を否定することは出来ません。
かなり分かり易く説明したと思います。それで文句があるようなら、
ソース云々などといわずに群論を勉強して下さい。
群論の学習法やテキストの例は>>1585から>>1590あたりで既に書きました。
繰り返しますが、もっと簡単なテキストでもよいです。
シュヴァレーのリー群論(日本語訳も出ています)は、書き方はともかく、
高校数学がしっかり出来れば、誰でも読める内容だと思います。
書き方は古いですけど、出だしは行列から話が始まっています(勿論、他の書籍でもよいです)。
一応、(+2)と(+3)の多項式の掛け算「(+2)×(+3)」の積は、原理的には「a×b=ab」と書いて計算することと同様に
「(+2)×(+3)=(+2)(+3)」と書いて計算出来ることは分かりますよね
(私は教師じゃないので正確には分からないが…)。
こういう計算の感覚が分かれば、>>1755や>>1756(いわゆる群論の考え方)の説明は分かると思います。
日本の教育委員会や大学教授、文科省を信用できないのに外人の群論を信用するのはなぜ?
ひねくれ物だからだよね?
群論を語る以前に自分自身が群論を誤って捉えてるだけでしょ。だから群論と一般教育では異なる部分がある。
って言うソースも無い、a÷bc=a÷bc=a÷b×cが公式と異なる点についてもスルー。
ソースが無いのだったら、ソースの在り方に文句言う前にソースが無いと認めるべき。
群論の立場は6÷(+2)(+3)=(+6)÷(+2)(+3)=(+6)÷(+2)×(+3)=…=9
普通に公式無視でしょ。
じゃあ6÷2√3を解いてくださいね。3√3にしかなりませんよね?
6÷(+2)(+√3)=(+6)÷(+2)(+√3)=(+6)÷(+2)×(+√3)=…=3√3
私は「文科省のカリキュラムだけが数学ではない」とはいった。
ソースを挙げることが数学ではないともいった。
それ以外で、大学教授が信用出来ないなどとはいっていない。
むしろ、大学教授は群論を知っている筈だよ。
>6÷(+2)(+√3)=(+6)÷(+2)(+√3)=(+6)÷(+2)×(+√3)=…=3√3
は群論では正しい。2√3を1つの数と見なして割算6÷2√3=6÷(+2√3)を計算したら、群論でも
6÷2√3=6÷(+2√3)=(+6)÷(+2√3)=(+6)÷((+2)(+√3))=…=√3
となって普通の割算の答え√3と同じになるよ。
安易に公式を認めてそれを使うことは、群論の立場から見たら1つの思い込みをしていることと同じ。
群論を使って考えるにあたってはソースなどどうでもよろしい。
まあ、シュヴァレーのリー群論はポントリャーギンの連続群論や松島先生の多様体入門の参考書になっている。
本当は行間が少ないポントリャーギンを勧めたいが、今は和訳が出ていないからね~。
シュヴァレーも書き方はともかく、論理的思考の練習にもなって読み易いとは思う。
解説も付いている。リー群論や多様体の古典になっている。
昔の人は(洋書の)ポントリャーギンやシュヴァレーで学習した位だ。
行列と群がセットで古典群として説明されている。例を出して群を説明しているから、分かり易いと思う。
私がおススメ出来る群論の最短の学習コースだ。
外国人の群論と日本人の群論が本質的に異なると思ったら大間違いだ。
ポントリャーギンの連続群論を読むことが私がおススメ出来る、
(分かり易さはともかく)群論の最短かつ最善の学習コースだ。
書き方は古いが、盲目の人が書いた本で、口で音読して読めるような書き方になっているから、行間は少ない。
第1章ですぐに群論、第2章で位相が出て来る。読むにあたっての前提知識も少ない。
ただ、残念ながら、今は日本語訳は出ていない。勿論、群論のすべてが載っている訳ではない。
内容については、昔の人のリー群(表現論)や多様体の教科書の1つにもなっていた位でマトモ。
ただ、今となっては記述というか説明が古くなっている。
群論を最短で学びたいなら、シュヴァレーでもポントリャーギンでもどちらでもよい。
(といっても、数学の洋書を読むことは、群論を知らない人に
とって難しいでしょうから、日本語の本の範囲で考えた)。
>(分かり易さはともかく)群論の最短かつ最善の学習コースだ。
は
>(読み易さはともかく)群論の最短かつ最善の学習コースだ。
といった方がよいかな。論理的思考力があれば、
(少なくとも群論の箇所の)ポントリャーギンの連続群論は理解出来る筈。
理解出来ないようなら、むしろ読解力に問題があると思う。
それ位に論理の行間は少ない。ただ、記号などの表記が今とは違う部分はある。
>むしろ、大学教授は群論を知っている筈だよ。
は
>むしろ、「(数学関係の)大学の先生など」は群論を知っている筈だよ。
というべきだったかな。単に大学教授といっても文学部など色々な人がいる訳で
どこまで群論を知っているか大学の先生がいるかまでは分からないな。
間違いなく、大学の数学の先生なら群論を知っていると思う。
>どこまで群論を知っている「か」大学の先生がいるかまでは分からないな。
は
>どこまで群論を知っている大学の先生がいるかまでは分からないな。
の間違いね。
人によって違う基準を述べている時点で確実に間違っていることを述べている人が存在することになる
上から引用:台湾のfacebookコミュニティにて算数の簡単な式を出題したところ多くの人が間違った解答をしたという
とあるので算数に群論を持ち込むべきではないのではなかろうか?
群論と群論ではない問題で基準が変わるなら
どちらの問題を出しているのかが分かるデータを示さなければ問題を区別できない
まともに読んでられない
あと2人の黒板に書いた途中式だと1という考えは6÷2(1+2)=・・1なんだけど
9の人の途中式は6÷2(1+2)と9が=でつながってないとのこと。
真相は知らないがつなげなかったのではと思われても仕方ないんじゃないか?
6の勝利のようだな
目の前にあるりんごの数は3個(1組+2組)=9個と考えることができる。
二つ目の解釈では6個のりんごを2人一組と2人2組の人数で等しく分ける。
2人1組=2人、2人2組=4人 2人1組+2人2組=6人
6個のりんごを6人で等しく分けると1人1個ずつと考えることができる。
肯定はするのは難しい・・としっかり書き込んでいるでしょう?
肯定するのは難しい≒信用できないってことでしょう。じゃあ群論も同様に肯定するのは難しいわけですね。
ソースは必要がないと散々言っているが、ソースがあるのか無いのかを聞いてるんですよ。
このネット社会で群論が一般教育と異なる場合があると書かれたサイトは存在するかを聞いてるんですよ?
分かります?だから無いなら無いって言えばいいだけなんですよ。
ソースが必要だってのは、説得力があるか無いかなんですよ。どこの誰だか知らず責任も無い人間の発言なんて
信頼できるわけないでしょ?
群論を活用していると言えば全く説得力が違うでしょう。
しかも公式を認めて使う事が思い込みなのは群論からすればそうなのかもしれないが、その過程で違いが出てきて
るんですよ?a÷bc=a÷b×cって言ってるでしょ?これは一般教育では間違いなんですよ。
2
6÷2(3)=6÷ー=9
3
じゃあこれを証明してください。
つうかこれとほとんど同じなんだがww
①肯定はするのは難しい・・としっかり書き込んでいるでしょう?
どこ?
②肯定するのは難しい≒信用できないってことでしょう。じゃあ群論も同様に肯定するのは難しいわけですね。
群論を否定するということは、数学の群論がうそになってしまう。たぶん、数学の根底の部分だよ。これを否定して成り立つ数学って…。ソースどころか、本も出版されているし、学問として成り立っているし、Wikiにもある。それこそ、探せば沢山あるんじゃないかな。大学のだれそれ教授のソース以上のものがみつかるよ。最低でも群論でぐぐってみ。それでも否定するなら、どうぞ。
とりあえず、答えを1に確定したいんですよね。なら、群論を否定する必要があります。群論的には9であるが、式がおかしいという結論になっているわけだが。なら、あなたは群論を否定するだけの理論をお持ちですか?少なくとも>>1760~1766はソースなど出さずに、自分の意見で発言しているわけだが。(教科書は出しているが、それを検証しているのが自分という意味で)。その上で、解説しているのだが。1の説明は、権威ある人が書いたソースと、公式だけ。
>>1775 でも大学教授が名前を出して群論を活用していると言えば全く説得力が違うでしょう。
a÷bc=a÷b×cが正解って、権威ある先生のソースがあったから、無条件に信じろ。こっちのほうが暴論です
検証は自分でやる必要がありますね。自分の意見として言うには。
群論を否定して成り立つ数学→聞いたことがない。
信用度としてはこれくらいありますが。
1の説明は、権威ある人が書いたソースと、公式だけ。
1775の説明は、権威ある人が書いたソースと、公式だけ。
に訂正します。すみません
Aが9となれば命題が証明されるだろうが、Aが1になれば証明されない。分数が入っているが、結局、6÷2(3)の解釈しだいなんだが、分数の式を入れる意味がわからないんだけど。後証明されるのは、6÷2(3)の解答が得られるかどうかですね。それがわからない限り、形を変えても同じだと思う。
ソースが必要だってのは、説得力があるか無いかなんですよ。どこの誰だか知らず責任も無い人間の発言なんて
信頼できるわけないでしょ?
は
どこの誰だか知らず責任も無いソースの発言なんて信頼できるわけないでしょ?
と言い換えることもできますが
群論を否定して成り立つ数学?
A÷BC=A÷(B×C)で成り立ってますよ?
これを認めて考えるのなら、>>1652や>>1654のような話になって問題の書き方が悪いっていう結論になるね。
「6÷2(1+2)」の答えがあるのなら、「6÷2(1+2)」の解釈で答えが異なるよ。
>>1756あたりでも書いたが、「6÷2(1+2)」と「6÷(+2)(+3)」は中身としては同じ式だ。
で、「6÷(+2)(+3)」だと「(+2)」つまり「6÷2(1+2)」の「2」と、
「(+3)」つまり「6÷2(1+2)」の「1+2」とを区別することが簡単に出来る。
群論の考え方はそういったことによる。
単純に「(+2)(+3)」つまり「2(1+2)」が1つの数と見れる訳ではないでしょう。
どちらかといったら、「2(1+2)」つまり「(+2)(+3)」では、
「2」つまり「(+2)」や「1+2」つまり「(+3)」を、それぞれ1固まりの1つの数と考えた方が自然だろうね。
「2(1+2)」と「1+2」の計算どちらが簡単かといったら、普通は「1+2」の方が簡単だと考えるでしょうね。
群論の最短の学習法も書いたでしょう。
何かこういうことばかりしていると自身の人生を台無しにするような気がして来たから、私はもうここには書かない。
というか、私を除いた群論を知っている他の人が何人か書いている。
くれぐれも、ソースがないことや公式「A÷BC=A÷(B×C)」を根拠にして
群論の考え方をすると答えがあるなら9になるということへの反論はしないでほしい。
6÷2(X+1)も2(X+1)を分母として考える。
実際、中高の数学ならこっちが正いはず。大学はしらんが。文系
特別に答えるが、「6÷2(1+2)」に答えがあるなら、沢山の人から見たら1であり、
群論の立場では9にもなるから、問題の書き方がおかしいという結論になる。
「6÷2(1+2)」は式として共通言語になっていない。
それじゃあね。
群論は、学問として成立していますよ。否定するなら学会で。
>>1796
問題の書き方がおかしいという結論になる。
私もその立場です。群論否定できたら、私は9という解答を引っ込めます。
補足。これは、一般的な意見ではなく私の意見です。
ソースと公式が数学だと思っている人がいるので、こういう書き方をします。そうだと思えば、それでかまいませんが、私自身は受け入れられません。数学とは何かって言う問いは、自分自身が考える問題だから。
そもそも探す気がない。
少なくとも学生の立場からしたらA÷BC=A÷B×Cとか言われても困るわ。
ソースは教科書や問題集でもいいんだろうか。
カッコは文字と同様に扱う。もちろん積として×の省略も可能。
ソースは教科書や問題集でもいいんだろうか。
それこそ星の数だけ存在する。日本国の算数で、文字式を学んでない小学生と、塾で文字式を学んだが、学校では文字式をまなんでない小学生。台湾で学んだ小学生や、中学、高校生もいるが、それら全て検証するの?それこそ無理だよ。だから、1か9が決定できないっていってる。
ある小学生A「塾で文字式学んだよー。」
Aの友人B「何それ、文字式なんて知らない」
ルール変わっちゃうね。
数学って大変だー。
と主張する人はゲームした時に某ソースを絶対視してルールの違いで揉めるだろうな。
6÷(1+2)=6÷1×(1+2)=18 が成り立つ。当然これは間違いであり、正しい解は、
6÷(1+2)=6÷3=2 である。これに倣って最初の式を考えると、
6÷2(1+2)=6÷(2+4)=6÷6=1 である。
なにも式の書き方がおかしいわけではなく、
a(b) と書かれている場合は、 {a(b)} であると理解すればいいだけのこと。
ニコニコ大百科に書いてあったこの考え方が一番スマートで説得力あると思うけどな。
6÷(1+2)=6÷1×(1+2)
6÷3から6÷1に変更されている
割る数が変更されている。
だからその考え方がおかしいから=9が真ならば・という説は違うんじゃない?
6÷1(1+2)=6÷(1+2)だもんね?
6÷(1+2) は 6÷1(1+2) のことであり、
6÷2(1+2) が 9 になる論理と同じ手続きをふんだら 6÷1×(1+2)=18 になるよ。
当然=18は間違いで=2が正しく、 6÷2(1+2) のような式を考える場合は、
6÷{2(1+2)} の{}が省略してるけど実際には在るんだな!と理解しよう。 ってことです。
みんなで統一したルールを築いていくのが数学だし、こういう意見交換は有意義ですね!
×{}が省略してるけど
逆に9側からしたら、勝手に式変えんなってなる。
9側は掛けるの省略を元に戻すのに、1側の都合しか考えてない。そもそも、積の省略をどうするかなのに、そっちができてから、1をかけてください。
6÷{2(1+2)} の{}が省略してるけど実際には在るんだな!と理解しよう。
勝手にカッコ増やした。それ、公式でしょ。
だから、1を否定できないっていってるじゃない。こっちは、逆に9を完全否定して欲しいんだけど。なぜ、左からかけてはいけないのか。
ごめんなさい。※1807よりも優れた説明が思いつきません。
がんばってくださいね。
>【9派の論理】
>6÷2(1+2)=6÷2×(1+2)=6÷2×3=9
>が正だとすると、【(1+2)に掛かる数が(省略済みの)1の場合】
>6÷(1+2)=6÷1(1+2)=6÷1×(1+2)=6÷1×3 = 18
>になるよ。これは当然誤りで、正しくは
>6÷(1+2)=2 でしょ
を引用して書いているようだが、これには致命的なミスがあるから指摘する。
今挙げたニコニコのソースの
>6÷(1+2)=6÷1(1+2)=6÷1×(1+2)=6÷1×3 = 18
という箇所は、正しくは
>6÷(1+2)=6÷(1(1+2))=6÷(1×(1+2))=6÷(1×3) = 6÷3=2
或いは
>6÷(1+2)=6÷((+1)(1+2))=6÷((+1)×(+1+2))=6÷((+1)×(+3)) = 6÷3=2
のような式を書いて計算をするんだよ。正しく訂正すると上のようになるんだよ。
こういう長らく放置されたミスが書いてあるソースを信じていたのか…。
だから数学をするにあたりソースはあてにならないっていったでしょう。
訂正すべき箇所とそれを訂正したものを書いた文は、>>1819に書きましたよ。
学校の先生とかなさった経験があるのでしょうか?
私はここで群論を持ち出して長らく書いていた>>1792です。
で、今日ニコニコをチラッと見たら、そこに間違いがあることがすぐ分かりました。
別に学校の先生でも何でもありません。そんな経験は特にありません。
このまま間違いが放置されていてはダメだと思って書きました。
6÷(1+2)=6÷(1(1+2))=6÷(1×(1+2))=6÷(1×3) = 6÷3=2 までたどり着けたなら、
※1807 の考えが理解できてもいいと思うんだけどなー。
6÷a(1+2)= における、
a=1 のときと a=2 のときの計算方法の違いにご自身で違和感を感じないのでしょうか?
数学をするにあたり違和感などという話を持ち出したら、>>1674や>>1675のような話になる。
普通、解析で「tanx=sinx÷cosx」などと書いたりして「÷」という記号は使いませんね。そういうのと一緒です。
勿論、群論で考えたら普通は余計な1など加えずに
6÷(1+2)=6÷(+1+2)=6÷(+3)=6÷3=2
などと計算したりする。
私は別に答えがあるならそれを1とする立場の否定はしていない。
群論で
6÷a(1+2)= における、 a=1 のときと a=2 のときの計算
位なら計算出来る。まあ、普通は「a=1のとき」なんて考えない。ただ式を複雑にしているだけ。
数学として考えると、6÷2(1+2)答えがあるならそれを1とすることばかり考えることはあり得ない。
正しくは「6÷2(1+2)の答え」でしたね。
答えがあるなら、群論で考えれば9にもなります。
個人の考えであってそういうのもあるよって話だから。
一般の考えでは1823さんが正しいけど群論を学べばそうとも考えられるよって事かな。
とりあえず一般の考え方では1807さんのは正しいと思うよ。
もしダメだとお思いなら是非、ニコニコ大百科の掲示板で議論してください。
それで他のユーザーに認められれば削除されると思いますよ。認められればですが。
ニコニコに書き込もうとしたら、メールアドレス云々の登録とか何か手続きが必要なようで、
私(ニコニコの記事を訂正した人)は、そこまでしてニコニコに書く気はしない。
例え登録したとしても、普段頻繁に書き込むことはないだろうと思っているしね。
記事は一応ボーッと眺めてはいたけど、今日少し真面目に読んだら確かにニコニコには訂正すべき箇所があった。
他に、某サイトによると文科省に「6÷2(1+2)」のような書き方をするか、本当に聞いた人がいるようで、
その人によると日本の義務教育ではそんな式の書き方はしない云々との話。
その人はサイトで叩かれまくっていたけどね。
まあ、数学的には答えがあるなら、9にも1にもなることや、電卓の機種で答えが変わったりすることからすると、
何か文科省に聞いたその人の話は正しいような気がしないでもないけど。
私は、登録してまでニコニコで議論する気はありません。
まあ、確率のパラドックスを持ち出したりして議論していた人などがいるようだけど、
まあ、中には(大学以降の)数学に通じたお方が書いていらっしゃることは確か。
だが、私は既にここで訂正すべき箇所は>>1819で訂正しました。
群論を知っている人なら、それで考えると
>6÷(1+2)=6÷((+1)(1+2))=6÷((+1)×(+1+2))=6÷((+1)×(+3)) = 6÷3=2
について
>6÷((+1)(1+2))=6÷(1+2)
となることはすぐに分かると思います。
>まあ、確率のパラドックスを持ち出したりして議論していた人などがいるようだけど、
>まあ、中には(大学以降の)数学に通じたお方が書いていらっしゃることは確か。
の部分は
>まあ、確率のパラドックスを持ち出したりして議論していた人などがいるようで、
>中には(大学以降の)数学に通じたお方が書いていらっしゃることは確か。
ですね。
1派・・1だ! 9だと矛盾が生ずる。
9派・・1を否定はしない(出来ない)けど9とも考えられる。
よって1なら問題なし。不備派はここにはいなそうだし。
そもそも、「6÷2(1+2)」(「6÷(+2)(+3)」)を「6÷(2(1+2))」(「6÷((+2)(+3))」)
と解釈しろと要求すること自体に無理がある。
群論を知っている人からしたら、これは「空気を読み過ぎだ」となる。
数学は多数決で決まるような代物ではない。
それを1ということばかりをやたら主張したがるんだろうか。
「6÷2(1+2)」(「6÷(+2)(+3)」)という式は人によって
解釈が異なることがあり、それ自体曖昧過ぎる式な訳なんだけど。
とっくに否定されてるがな・・。
群論で考えると、解釈は殆ど限定されて来るといっていいから
群論で考えている人があたかも1人であるかのように見えるだけだよ。
確実に、群論で考えているような人が数人はいる。
以前もう書かないじゃあね と言ってた人?
私=>>1838(など)はそう。昨日は「6÷2(1+2)」については全く書いていない。
少なくとも、昨日書いていた人や>>1835は、自身とは異なる別人。
(ここのサイトから)じゃあねww
ニコニコに致命的なミスがあり、それを訂正するために書いた。
私は今まで内容が間違ったソースを挙げて
答えが1だとばかり主張する人を相手にしていたのか…、
って感じで気分が虚しくなっているよ。
一体ここに書いたことに何の意味があったんだろうか…、というような感じでね。
>ニコニコに致命的なミスがあり、
は
>ニコニコに致命的なミスがあることに気付き、
ですね。
まあ、ソースを挙げるときは、その中身の正しさを検証すること位はしましょう。
これは、ソースに基づいて真偽を議論する上ではとても重要なことです。
私は、>>1842のように虚しさを感じて来て、これ(「6÷2(1+2)」)について書く気が失せました。
最初 台湾の記事のとおり9だと信じて1派を馬鹿にしまくってたんだろうな。
あとからニコニコ大百科で1派優勢になってきたから群論とか一般的でない言葉を使ってごまかしながら、
1 も 9 も両方いえるという論に切り替えてそれをキープすることでなんとかしようと思っている。
自分の論理矛盾を認めちゃったら9がいえなくなるもんね!
といい、
※1819 で >6÷(1+2)=6÷(1(1+2))=6÷(1×(1+2))=6÷(1×3) = 6÷3=2
と説明してるけど、
※1807 の3行目を無視して同じこと言ってるだけだよね。
6÷a(1+2)= が a=2 のときでも、同じく 6÷(2(1+2))= とし、 1しか導けなくなることを知ってるはずなのに、そこを9もあるというのが病的な人に思えてならない。
お疲れ様でした。
あーあ、代入しちゃった。元の式を文字式の置き換えて、式を変えて証明。しかも、方程式に。証明以前の問題だ。
普通に合ってるし。
群論乙☆しかし何でまだいるんだよ・・。
だね。なんかもう、何回もおんなじこと説明してる。わたしも、左からかけて9、一般的には1となるので、式がおかしいが最終結論です。あと、群論的(数学的な根拠)もわかりました。後、ソースと、公式を無条件に受け入れるっていうことがどういうことかもわかりました。ネットで、適当に証拠集めして、数学もどきをつくってください。なんかいろいろ疲れた。これだけ議論できたので、後は皆さんに任せます。これ以上の議論は私にとって無意味です。
待ってよ待ってよ。群論とソースと公式についてもっと語ってくださいよ。
それは公式だよね?だと言って否定している意味もさっぱりわからないし、もっと具体的に説明してよ。
とりあえず 群論ってどういう学問なの? 導入だけおねがい。
[1] 6÷2x の x に 1+2を代入するとどういう形になりますか?
① 6÷2(1+2) ② 6÷2×(1+2)
[2] 6÷x の x に 1+2を代入するとどういう形になりますか?(当然xは1xを意味しています)
① 6÷1(1+2) ② 6÷1×(1+2)
スルー
電卓は計算する機械であって、計算する順序は人間が考えないといけない。
機械が正しかろうが9以外の答えの人は
やっぱこれ式がおかしい笑
A÷BC=1
A÷B×C=9
って事だ。つまり文字式でもないのに×も・もないから混乱したわけだ。
みんな難しく考えすぎたな笑
A=6
B=2
C=(1+2)
だから、 6÷2(1+2)=1 ってことでしょ。
小学校先生:(1+1=2)です。
小学生エジソン:1個の粘土と1個の粘土を合わせたら、大きな1個の粘土になるじゃん!(1+1=1)
と抽象的には一緒。そもそも定義が違うのだからそりゃ噛み合わんわな。
数学というのはそういう帰納的な判断で終わらせるのではなく、演繹的に答えを導くものなのだがな。
演繹的に答えを導くために根拠となる定義をするということだな。
中学校の教科書で定義は与えられてるからね。 6÷2(1+2)=1 なの。
中には6÷2を一つの数として見て、2(1+2)を一つの数として見ていない人もいるようだが。
俺は今後も2(1+2)を一つの数として見て問題を解いていくつもりだ。
1だよ
深沢真太郎 [BMコンサルティング・代表/ビジネス数学コンサルタント]という人がウルトラCの恥を晒してしまったってことでいいのでしょうか?
何かすごい事が書かれてるのかと思ったら6÷2(1+2)=6÷2×3=9
これだけ??で、とっくにこんなことは初期の通過点なわけだが※1870は
これを見てどうしろといいたいわけ?
2×3を文字式のように省略したら2×3=23となってしまい、
通常の表記に反して間違った式の表記になって2×3を省略して23などとは書けないから
敢えて2(3)という通常は書かない表記の式を積と読んでいることが分からないような人達が
強引に1であることを主張しているネットだからね。
失礼。
>敢えて2(3)という通常は書かない表記の式を積と読んでいること
も
>敢えて2(3)という通常は書かない表記の式を積と「呼」んで「定義して」いること
と訂正。
積とかソースとかニコニコとか2(3)とか持ち出して・・まさかね。
~fZさん?ちなみに1878の主張はとっくに論破されてますよ。
違うよ。傍観していただけ。未だに訂正もされていないじゃないか…。
掛け算の「×」という記号が省略されて「2×(1+2)」という数式が
2×(1+2)=2(1+2)
と省略されて書かれるに至った歴史的背景があることから
答えが9であることを主張していた人がいたんだけど、
そういう歴史的背景があるのなら、尚更答えがあるなら9とした方が自然になるよ。
そういうことは今まで知らなかったんだけどね。
まあ、数学の論理に歴史をやみくもに持ち込んで論理的思考をすることはよくないだろうけどね。
あとね、k(キロ)というのはmやm^3とか他の単位の前に付き
kmやkm^3などと他の単位になって(mやm^3などの)1000倍の意味を表す
ようにする接頭語であることを知っているのかどうかは知らないけど、
反論するにあたり、k(キロ)を接頭語ではなく代数的文字と見なしているようなんだよね。
そういうことからも、反論にはなっていないよ。
他にも「cos」という記号を「c×o×s」と文字の掛け算で表してみたりさ。
こういうことはあり得ないよ。
「k」という接頭語や記号「cos」を仮に知っているなら、意図的にそういうことをしているとしか思えない。
いや、「km^3」は単純に「m^3」の1000倍ではなく
m^3の(10^3)^3=10^9倍だから、>>1884の説明で例としておかしかった。
m(メートル)とかl(リットル)など、自身の前に付いて
km(キロメートル)やkl(キロリットル)などとなって
1000倍を表すk(キロ)や0.01倍を表すc(センチ)などの
新しい単位のもとになる接頭語が付くような、一連の元々の単位がある
(SI単位系だっけ?正確な名称は忘れました)。
例えばcm(センチメートル)も1mの0.01倍でそう。
まあ、>>1884の「m^3」は「l(リットル)」、「km^3」は「kl(キロリットル)」にそれぞれ変更です。
ニコニコの議論ならニコニコでやればいいじゃん。
ここでいきなり意味不明な発言されても困るよ。
意味不明ってね~、簡単な単位のお話だよ。
まあ、ニコニコでも見てみなよ。
頑なに1であることを主張している人達は、>>1884のようなことを考えているんだよ。
頑なに1であることを主張している人達は、ちょっと読解力がないんじゃないかな~って思っている訳。
ニコニコで議論する気はない。
見てみたけど、9を主張する人が逃げて書いてないだけじゃん。
ニコニコでは議論できないが本音でしょ。
意味不明ってのはなぜいきなりkキロとか持ち出すのか。
何でここで偉そうに書き込むのかその思考力がわからない。
あなたが主張すべきはニコニコ内でのはず。
論破や集中砲火を恐れて書き込めないのがまるわかり。
単位の話は、物理かなんかを知っている人なら分かると思うよ。
高校かなんかで>>1884や>>1885のようなことはやったと思う。
一応分かり易く書き直すとね、>>1885の途中の部分は
>m(メートル)とかl(リットル)など「がそうであるように」、自身の前に付いて
>km(キロメートル)やkl(キロリットル)などとなっ「たりするなどして、」
>1000倍を表すk(キロ)や0.01倍を表すc(センチ)などの
>新しい単位「と」なる接頭語が付く「ことで新しい単位になる」ような、一連の元々の単位がある
となる。例えば、l(リットル)という単位にd(デシ)という0.1倍を表すような接頭語を付けることで
dl(デシリットル)という、単位量あたりl(リットル)の単位量の0.1倍の量を表すような、別の単位になる。
m(メートル)やl(リットル)の他に、g(グラム)という単位もこれらと同様の種類で然り。
少し前のスレまでたどって見てみるとよい。
頑なに1であることを主張している人達の中には、>>1884のようなことを考えている人がいる。
群論を持ち出してニコニコで議論しても、頑なに1であることを主張している人達には分からないと思うよ。
ニコニコに書く気はない。
書けない。怖くて。が本音でしょ。
9だとおかしくなり矛盾が生ずることに対する指摘に答えず
こう考えれば9となると言い訳ばかりで矛盾に対する答えが無い。
>9だとおかしくなり矛盾が生ずる
9とする立場で論理的に考えるにあたりどこでどのように矛盾が生じるんだい?
一応、「9とする立場」というのは、「仮に答えがあるならそれを9とする立場」のことね。
群論を主張してきた人でしょ?あなたの考え方自体が間違ってるんだよね。
なぜ今回は群論を言わないの?
まず公式に反している。静岡大教授のがソースね。ソースと聞くと拒絶するんでしたっけ?
A÷BC=A÷B×Cと考えてるから・・があなたの言い分でしょ?
でもこれは間違ってるんだよね。A÷(B×C)と解かないといけない決まりがある。
決まりを守らないで好き勝手な考え方してこうとも言える。まずは最低限のルールを学ぼうよ。
ニコニコ掲示板で文句言ってくださいね。
ニコニコでは怖くてできないから、ここでニコニコの文句を言うの?
自信がないから怖いだけなのがまるわかり。情けないよ。
>>1898
やっぱり分からないようだね。
群論では積という言葉は、例えば「(+2)(+3)」という積は、「+2と+3の積」という
(これでも正確ではない部分は残る)訳で、
正確にいえば単純に「(+2)(+3)」を「積」ということはしない。
あと、(+2)(+3)に等しい「+6」は、1つの数を表すような表記になっている場合なんかは、
論理的には積と呼ぶことが可能でも、普通は積+6とはいわない。
>>1898
(続き)
そういうことをし出したら、(+1)(+6)=+6なんだから、
「+6」を「+1と+6の積」などともいえるようになったりして、キリがなくなる。
普通は「+6」などという表記をされた数については、「1つの元+6」とか「1点+6」などといったりする。
つまり、群論でいう積が指し示す対象と義務教育でいう積が指し示す対象は
本質的には同じであっても、その表記が変わったときの扱い方の点で微妙に異なる。
よって、群論で考えたときと普通の割算で考えたとき、答えが異なるのは当たり前。
義務教育の論理を群論の論理に照らし合わせたら、矛盾が生じて当たり前。
群論の論理を義務教育の論理に照らし合わせると矛盾が生じることも同様。
公式と違うよ、公式無視なのにね。
で9とも言えると言い訳ばっか。
群論ではなく一般教育課程で書き込んでください。
群論と通常の義務教育で異なる ソース をお願いします。
あと積の話はニコニコでの議論でしょ?9派の人はまだ書き込んでない
みたいだし、そちらでどうぞ。逃げたんでしょうが。
それじゃあ群論は学問として日本では認められないね。
義務教育は義務だからね。義務に反しちゃダメだね。
>>1898
(続き)
ソースね。まあ、マトモな群論のテキストなら何でもいいと思うよ。
ポントリャーギンの連続群論か、シュヴァレーかなんかでいいんじゃない。
>>1898
1年近く某サイトで同じような議論したから、
今更ニコニコに登録してまで同じような議論をする気はないよ。
大学の数学の先生からしたら、そんなこといったりしたら、
「何いってんだ!!!このバカモノ!!!」
っていい出すだろうね。
それ位までに、群論は現代数学の基本になっている。
そもそもの出だしの定義が全く違うんだから、
片方の論理の視点から見たら、他の片方は矛盾することになって当たり前。
平行線の公理を巡って生じた3種類の幾何学なんかと同じ。
3角形の内角の和は丁度180度、180度より大きい、それよい小さいなんていう幾何があるが、
それぞれの幾何の視点の論理に照らし合わせて他の幾何を論理的に考えているようなモノ。
群論は確かに認められてるんだろうが、群論が一般の教育と異なるならソースがなければ
逆におかしい。そもそも群論の捉え方自体を間違ってるんじゃないの?
それで静岡大の教授については受け入れられない?大学の数学の先生も受け入れるなよ。
そもそも球体の表面上に直線を引ける群論理論者が平行を語るのは間違ってます。
1年近く議論して全く受け入れられてないんですね。まあわかりますが。
直接的に群論が一般の教育と異なることが群論のテキストに書かれている訳ないだろう。
それを見て割算を群論の立場で再構成することに意味があるんだよ。
そうすれば、仮に6÷2(1+2)に答えがあるならその答えは9になる。
群論を理解していれば特別に難しいことではないよ。
いい加減ソース主義もやめてくれよ。
なんか数学の閃きにもソースがあるとでも思っていかねないな。
(補足)
まあ、
問題:割り算6÷(1-1)√2に答えがあるとします。そのときの答えを求めなさい。
なんていう類の問題は、仮に群論で考えて計算出来るとして計算しても
6÷(1-1)√2=6÷(1-1)×√2=6÷0×√2
となってこれ以上計算出来なくなるから、
群論で考えても計算して答えは求められないけどね。
まあ、義務教育では割り算6÷2(1-1)は、問題として考えないことと比較すれば、
普通の読解力がある人なら>>1910(>>1911)の趣旨は分かるでしょうね。
義務教育では、割り算6÷2(1-1)を計算するようなことはしないことは分かるよね。
義務教育の考え方は、6÷2(1-1)での割る積2(1-1)を0と考える立場だからね。
では群論自体は義務教育と違うところは存在せず、勝手に自分で群論と義務教育は違う。
そう閃いた、個人の考え方ですよね。
好きにすればいい 。
もはや、頑なに1と主張する人は、救いようがなくなってきた。
群論には義務教育と違うところなんていっぱいあるよ。
巡回群や準同型、位相群なんて義務教育では考えないだろう。まあ、
>勝手に自分で群論と義務教育は違う。そう閃いた、個人の考え方ですよね。
なんていうのは閃きでも何でもなく、単なる拗けた解釈に過ぎない。
某サイトで議論したときは、同じ答えがあるなら1とする(数学専攻ではない)人でも群論を知っていて
頑なに1と主張することばかりするようなことはしない人もいたんだけどね。
勿論、頑なに1と主張する人もいたけどね。なんか相手していて呆れてきたよ。
「分母が0ではない(正の)整数、分子が整数からなるような分数」のことね
(これで分かる筈だが…)。
もし分からないようなら、「有理数」を「小学校レベルの分数」と置き換えて読んでいい。
6÷3分の2=1になるんでしょ?
6÷2(1+2)=9派のあなたの考えでは。
>6÷3分の2=1になるんでしょ?
式の表記が曖昧で、原理的には
>6÷(3分の2)=9
とも
>(6÷3)分の2=2分の2=1
とも解釈出来る。まあ、普通の読解力がある人なら
「3分の2」なんて書いてあれば、それが分数であることが読み取れるから
>6÷(3分の2)=9
と解釈出来るでしょうね。
>6÷3分の2=1
という書き方が
>(6÷3)分の2=1
という意味を指して書かれてある文章は、ちょっと見たことがない。
それこそ(いわゆる多くの人にとっての空気を読んで)普通の読解力があれば
>6÷(3分の2)=9
と解釈出来る(筈)。
ポントリャーギンの連続群論かシュヴァレーのリー群論
でも読んでからにしてほしい。
それじゃあね。
6÷2(1+2)=9 と主張してた間違いに気付きながら、それを素直に認めようとせずに、
群論という2段も3段も難しい言葉を使って煙に巻こうとしてる姿勢が気にいらないんだよね。
しばらくすると出てくる。いったい何なんだ?
>ニコニコでも全く同じ展開だったけど
>つまり6÷3分の2は9なんだよ。
それは単なる(空気を読んだ)勝手な思い込みに過ぎない。
論理的に考えると、原理的には>>1928のように2通りの解釈が出来る。
もっと論理性を鍛えた方がいいんじゃないの?
というか、一体何をキレたような口調で書いているんだ?
群論を用いた考え方を噛み砕いて分かり易く説明したとは思うんだけど、
仮に答えがあるなら1とばかりいう人は、それが分からないようなんだよね。
感覚としては算数で「6÷2(1+2)」を計算するような立場に近い。
>>1933
このようにアルファベットの文字が入った単項式の割算なら、
日本社会の習慣に合わせて考える限りでは、一々群論を持ち出すまでもなく、
普通に義務教育の方法で計算出来ますね。勿論、群論で考えることも出来ますけどね。
だが、「6÷2(1+2)」では単純にそういう日本社会の習慣に合わせるようなことは出来ない。
一体答えを9にしたいのか1にしたいのか、どちらにしたい表記の式なのかよく分からず、
ちょっと空気の読みようがないですね。
その立場には、群論だけでなく、歴史的背景という2つの根拠があることになってしまった。
その他にも電卓の機種で答えが違うらしいなど、1とした方が自然と考えるには確固たる根拠はない。
主にあるのは流動的な学習指導要領の内容だけ。
掛け算「2×(1+2)」の「×」が文字Xや文字xと解釈されかねず
「2×(1+2)」と「2X(1+2)」や「2x(1+2)」で誤解が生じかねないから
「2(1+2)」と表すことで掛け算「2×(1+2)」を指すに至った
という歴史があることは分からなかったんだけどね。
2×(1+2)=2(1+2)
なんだから、その両辺に直接左から「6÷」を付ければ
6÷2×(1+2)=6÷2(1+2)
つまり
6÷2(1+2)=6÷2×(1+2)
という式が得られる。そういう解釈をすることが出来る。
1年近く、散々1とばかり主張する人を(主に1人で)相手していて、こっちもいい加減疲れてきたんだよ。
>>1942では主観的感情を他人にぶちまけるようなことをして、どうもすみません。
まあ、ここまで答えを1と頑なに主張しているような人がニコニコを支配しているようでは、
ニコニコで「…バカが支配しているからねw…」
などと書く人が出て来てもしょうがないでしょね。
こういう人達には、ちょっと拗けて考え過ぎているか、かなりの読解力不足の人がいます。
厳密な解釈をしたりしている点や、知識や書き方などからすると、ちょっと小中高生とは思えないですね。
そもそも、ニコニコはソース至上主義の考え方をしている限り、
ソースが不十分で議論不足なようでは、>>1943のように
答えを1と頑なに主張するような人がニコニコを支配するに至る可能性が高い仕組みになっている訳です。
一応ニコニコのソースを見ては見ましたけど、日本語のソースは多いけれども
肝心の台湾や他の外国のソースが少ないので、
>「単項式どうしの除法」は、北米でも台湾でも日本と同じルール→[F01][F02]
と結論付けるにはまだ根拠不足なんです。
肝心のそれらの国のソースを増やして議論しないとソース至上主義をしても意味がないんです。
で、ソース至上主義をしておきながら、外国のソースも否定してしまう?
それではニコニコはどうしようもないですよ。
(続き)
某サイトで議論していたときは、「6÷2(1+2)」に答えがあるなら9とする方が妥当云々
などという内容の日本語の論文を挙げたりする人がいて、マトモな人がいましたね。
すぐにその論文を挙げることは出来ないですけど、もし興味があるなら検索して調べて下さい。
ネット上にある筈です。
まあ、長々と色々ボヤいて、大変申し訳ありません。
2×(1+2)=2(1+2)=6なんだから
6÷を頭につけるなら2×(1+2)は{}をつけないとダメだろ?
それがないなら6÷2×(1+2)=6÷2(1+2)=6÷6
になるだろうが。正確には
6÷2×(1+2)≠6÷2(1+2)=6÷6
>2×(1+2)=2(1+2)=6なんだから
この理屈が通用するなら
(+2)×(1+2)=(+2)(1+2)
という式についても通用しないといけないんだが、このときはどうする?
計算して値を求めなければ>>1941のようなことは出来る。
だからそのソースか使用例を
>>1967
サイトやソースなんてない。
こういうことは、マトモな群論を学習した上での、ちょっとした理論構成だよ。
いわゆる研究ってい得るかどうかは分からないけど、それに似た代物ね。
>>1966
>>1783は別人ですね。
>いわゆる研究ってい得るかどうかは分からないけど、
は
>いわゆる研究ってい「え」るかどうかは分からないけど、
と訂正。
>>1969
いわゆる群論の簡単なお遊びか応用だか知らないけど、そういう代物の1つ。
しいてソースを挙げるとすれば、マトモな群論のテキストになる。
2(3)を使用例がないからおかしいと言ってたので
当然本来、分数には()をつけるというあなたの主張にはさぞかし
使用例が多いんですよね?それを教えてと言ってるだけですよ~?
その前に、群論を勉強して、自分で理論構成しておくれ。
というか、1とばかり主張する人のために、
分数についての根性を叩き直してくれるような代物を教えてあげるよ。
群論とは関係なくなるけど、取り敢えず岩波書店の「解析学の基礎」ね。
これやれば、脳ミソが鍛えられて、分数についての見方は変わるよ。
その著者が書いた書籍の参考文献の中に、私が挙げたポントリャーギンの連続群論があるんだよ。
それ位にポントリャーギンの連続群論はいい本なんだよ。
謝罪するなりしなさいよ~
サイトやソースはないですね。
どちらかというと、論理的に話を組み立てている作業です。
岩波書店の「解析学の基礎」もそういう構成に近いです。
沢山の人にとっては、間違いなく鬼畜以外の何物でもないですけどね。
どこのアスぺが分数にいちいち()つけるんだよ。
でも9派の考え方では=にならないとおかしい。
言い訳が意味不明でルール無視
確かに9ではおかしい部分もあるんだろうが、こう解けば9!
でいいだろ。そんなに否定したがる理由がわからないよ。
ぐんろん!
数学において、一つの問題に対して2つも3つも答えが導けるというのはありえないことなのです。
6÷2(1+2) とした場合、因数分解の前後で解が変わることは無いので「9」が解になることはない。
∴6÷2(1+2)=1
で解決じゃないの?確かに式がおかしいけど、9になる方の証明は俺の頭じゃできなかった。
まさかぐんろんだったりして。それはそれで面白くなりそうだ。
あんた! 天才だな…
やるな、正論
群論の考え方でそれを正確に書くと
>6÷(2+4) の括弧内を因数分解して
>6÷(2(1+2)) とした場合、因数分解の前後で解が変わることは無いので「9」が解になることはない。
>∴6÷(2(1+2))=1
>で解決
になるからね。つまり、で出だしで「6÷(2+4)」という式を書いている時点で
暗黙のうちに義務教育の考え方をして6÷(2(1+2))=6÷(2(1+2))を仮定してしまっている訳。
真似なんかしてはいない。
一々他のサイトの記事を見て、それを真似て同じことを書いても意味はないだろうよ。
こんなバカバカしいことはやってられないよ。
感覚としては、そういった類のことは、何も考えずに文章を書くような作業に近い。
>>2001の「つまり、で出だしで」は「つまり、出だしで」と訂正ね。
これまで答えがあるなら9とすることも出来る群論の考え方を理解したいなら
群論の学習をした方がいいといってたんだよな。
ポントリャーギンの連続群論やシュヴァレーのリー群論とか分かり易いテキストも挙げた。
>>2002だと群論の初歩を全く知らないと理解出来ないだろうからね。
分かると思っていたんだが、>>2003のような式の書き方では伝わらなかったようだ。
お前は小学のさんすうドリルをやれ!!
趣旨がよく分からないが、2人の数学者の名前を両方間違えているところからすると、
もしかしたら群論を知らない人かもね。
位相群やコンパクト群や行列表現などの群論を知っている人なら、
2人の名前を両方間違えることはない筈なんだよね。
1行目の前半と2行目の後半とでは内容が全く違う。
算数(文字式の計算を含む)で「6÷2(1+2)」の類の式は計算したことがないんだよね。
後半は私=>>2006にいってるの?
>>2010の
>やはり前半の推測は正しそうだね。
は>>2008の話ね。
群論を理解していたら、考え方は小学校の算数の考え方をして、
「6÷2(1+2)」に答えがあるなら9と考えるようになる。
>>2010の
>「シュプール」を行列の「トレース」に置き換えて読めたりすることが出来る筈なんだよね。
は
>「シュプール」を行列の「トレース」に置き換えて読んだりすることが出来ることになるんだよね。
と訂正。「シュプール」は「トレース」の古い呼び方。
ポントリャーギンもシュヴァレーも、位相群上のフーリエ解析(調和解析)、或いは有限群で群論に貢献した人だから、
群論を或る程度知っている人なら、2人の名前を両方間違えることはない筈。
ポントリャーギンやシュヴァレーの名前が付いた用語もある。
義務教育なんてバカバカしくてやる気がないし、そういうのをしている時間はない。
やはり、>>2007とか>>2012とかは、答えが1とばかり主張する人なのだろうね。
でもおまえが小学のさんすうできないことはわかった
なんで
2
6÷―ー=6÷(2÷3)
3
で()がつくのに6÷2(3)=6÷2×3になるの?
その考えなら6÷(2×3)が正しいよね
違う、6÷2(3)について。
その考えなら6÷2×3じゃおかしいよ。
6÷(2×3)じゃないと。
なんで分数の時は6÷(2÷3)と()つけてるのに。
>>1つの分数を1つの数と見なすことは出来ないのか?
同様に2(3)を1つの数とみなせます。
2(3)を1つの数と見なす立場が可能なら、2と3が別々の数と見なすことも出来る。
群論の考え方では、最初は2=+2と3=+3を別々の数と見なし
(+2)×(+3)と(+2)(+3)を=という記号で(+2)×(+3)=(+2)(+3)
と結ぶことで(+2)(+3)という1つの数を構成する。
「(+2)×(+3)=(+2)(+3)」は「×((+2)、(+3))=(+2)(+3)」
と書いてもよいが、この「×((+2)、(+3))=(+2)(+3)」という表記なら、
群論の考え方でも必然的に「6÷(×((+2)、(+3)) )=6÷((+2)(+3))」
言い換えれば「6÷(2(1+2))=6÷((+2)(+3))=1」という解釈をすることになる。
(続き)
だが、普通は四則演算の式を書くにあたり「6÷(×((+2)、(+3)) )」などという表記はしない。
そういう表記をしたら逆元とかを考えるとき不便だ。
これなら単純に「6÷((+2)×(+3))」などと書いた方が簡単だ。
で、群論では通常は×と÷、及び省略された積の優先順位は同じと考える。
やっと頑なに答えが1と主張する人の考え方が見えて来た。
多分頑なに答えが1と主張する人は×という二項演算を用いた「(+2)×(+3)=(+2)(+3)」という
(群論でいう)積を定義する変換(いわゆる同じ集合からその集合への写像)を用いて
「×((+2)、(+3))=(+2)(+3)」などと書いて考えているのかも知れない。
>>2024の「×((+2)、(+3))=(+2)(+3)」などと書くようなことは出来ないか。
一応(群論の考え方をして)その表記で「6÷(+2)(+3)」つまり「6÷2(1+2)」を書くと、
6÷×((+2)、(+3))=6÷(+2)(+3)
つまり
6÷×(2、1+2)=6÷2(1+2)
と書くことになって、四則演算を表す式にしては、何か奇妙な表記をしていることになる。
積=乗法の解だよ?
解を省略するってこと?意味がわかりません。
ここが意味がわかりません。ソースはお嫌いなようですが、ソースが無ければ納得できません。
群論ではそう考える その類の物を示す証拠はありますか?
また÷の省略ー に関しては×、÷より優先させるんですよね?×の省略と÷の省略では優先順位に
違いが出るものなのでしょうか?
>(群論でいう)積を定義する変換(いわゆる同じ集合からその集合への写像)
は、正しくは
>(群論でいう)積を定義する写像(1つの空でない集合Gの直積G×GからGへの)
ね。
よく分かってんじゃんその無理数が入った分数と同じ考え方をして6÷2(1+2)を計算するんだよ。
そうすると9になる。
矛盾を指摘されてそれと同じ考えで解くとかww
あっ、そうそう。あのね、大学の講義でする数学だけが数学ではない。
これは義務教育でする数学だけが数学ではないことがいえることと同様に、
大学の(数学科の)講義でする数学だけが数学ではない。
時間的制約などから、大学で行える数学の量には限界がある。
一応ね、これは肝に銘じておいた方がいい。
2
6÷―ー=
3
とかは群論を使った考え方をしてはいけないんだよ。
群論で考えるにはこの式は解けないことだな。
よっぽど決まりも何もない学問だと思うが
あと、自分も省略された積という表現が全く理解できません。
それこそ群論を学習して、「×」や「÷」を再構成してみておくれ。
群論では、掛け算「a×b」などとはいわず、「a×b=ab」の両辺を積という。
そこで右辺の「ab」を、本来は「aとbの積」というべき式を「省略された積」と呼んでいる。
それだけの話。
検索しても出てこない。勝手に呼んでるだけ
積自体が省略された意味になるからね。
それこそ自分で理論を(再)構成するようなことに近い。
このようなことは大半の人はやらないだろうから、私のいっていることが分からないだけだと思う。
そのような(再)構成をするような内容になっているのが、
>>1976で挙げた「解析学の基礎」や「函数解析と微分方程式」ね。
まあ、これらをこなせたら、間違いなく「÷」なんていう記号は使わなくなるよ。
定理の証明を0から始めて行くような代物だからね。
中には定義を書かせるような問題が演習問題になっている部分もある。
厳密にいえばそうなる。
或いは「記号を省略して表した積」となる。
俺様が群論で考えて解けばこうなるはずだ!だからこの主張を認めろってことだよね・・
マジなのか・・
どちらかというと、群論で割り算や掛け算を再構成することは、
既存の群論の一般論の1つの例を考えるようなことに近いんだよ。
つまり、群論に当てはめて考える限りでは、必然的にそうなってしまう訳。
「こうなる筈だ」ではなく、「論理的にいえる」ことになる。
だから、その内容は義務教育とは違ってきて当たり前。
あと、「解析学の基礎」や「函数解析と微分方程式」は、むやみに手を出さない方がいいとは思うよ。
実解析を扱う内容は弱い部分があるが、或る程度は前提知識がないとスラスラ解くことは難しい。
全体的には、むしろ微分方程式に焦点を合わせた内容になっている。
少なくとも、実解析なら「解析学の基礎」より遥かによい代物がある。
いや、部分によってはかなりの前提知識がないと、これらはスラスラ解けないな。
何せ定義を書かせるような演習問題がある位だからね。
俺様が群論で考えて解けば論理的に言える!だから義務教育は間違ってる!
やばいだろ・・
かつま「……だめだこりゃ!」
理論の再構成まで言ってしまったら論点がまったく違ってくるんだけどな。
つまり、論点を元に戻せば 6÷2(1+2)=9 はないってことでオッケーじゃん
この件についていえば群論なんて解らなくてもいいんだよ。
「理論の再構成」 がしたいのなら、大学教授にでもなってくれ。フィールズ賞もらえるぞ♪
群論を語る人の意見は9
決して群論が9なわけではない
6÷(1+2)=6÷1×(1+2)=18 も真のはず。
が、こえは当然間違っており、正しくは
6÷(1+2)=6÷3=2 である。
これを説明できないかぎり、群論は意味が無い。
説明しましょうか。群論の考え方では「6÷(1+2)」の「÷」の直後の
(いわゆる普通の人にとっての割る数)「1+2」について
1+2=(+1)(1+2)
です。これは群論の考え方でも成り立つから
t=1+2=(+1)(1+2)
とでも置き換えることが出来ます。そう置き換えると「6÷(1+2)」は「6÷t」となります。
ここで「t=1+2」と置き換えたのだから、群論の考え方では、
「6÷t」を元に戻すときは「1+2」を括弧()を用いて「6÷(1+2)」と戻します。
そうすると最初の式の「6÷(1+2)」になり、何も問題はありません。
一応
>そう置き換えると「6÷(1+2)」は「6÷t」となります。
>ここで「t=1+2」と置き換えたのだから、群論の考え方では、
>「6÷t」を元に戻すときは「1+2」を括弧()を用いて「6÷(1+2)」と戻します。
>そうすると最初の式の「6÷(1+2)」になり、何も問題はありません。
の部分に注意しましょう。これと同様に、
「t=(+1)(1+2)」と置き換えたのだから、群論の考え方では、「6÷t」を元に戻すときは
「1+2」と等しい数にあたる「(+1)(1+2)」を括弧()を用いて「6÷((+1)(1+2))」と戻します。
そうすると、最初の式の「6÷(1+2)」に等しい式「6÷((+1)(1+2))」が得られます。何も問題はありません。
そこで「6÷(1+2)」と「6÷((+1)(1+2))」を等号「=」で結べば「6÷(1+2)=6÷((+1)(1+2))」となります。
>>2069で置き換えた
t=1+2=(+1)(1+2)
について、「t=1+2」と「t=(+1)(1+2)」を元に戻して「6÷t」を最初の式に戻すときは、
どちらも同じ考え方をしているので、最終的には
6÷(1+2)=6÷((+1)(1+2))
となるため、
>6÷2(1+2)=6÷2×(1+2)=9 が真ならば、6÷(1+2)=6÷1×(1+2)=18 も真のはず。
は間違いであり、正しくは
6÷(1+2)=6÷((+1)(1+2))=2
というようになります。
もし分からないようなら、ご自由に
>6÷2(1+2)=6÷2×(1+2)=9 が真ならば、
>6÷(1+2)=6÷1×(1+2)=18 も真のはず。
を認めちゃって下さい。
「6÷2(1+2)」いわゆる「6÷(+2)(+3)」なんていう表記の式の問題出されたら、
「6÷(+2)」(つまり「6÷2」)を先に計算させたいのか、
「(+2)(+3)」(つまり「2(1+2)」)を先に計算させたいのか、
ちょっと理解に苦しむよ。見方によっては「6÷2」を先に計算させたい、と捉えることも出来る。
そういう出題者の意図を判別しかねる表記をしている問題で、問題の表記がおかしいといっている訳。
まあ、後はご自由に書いて下さい。
私自身、派手に議論し過ぎたと思っておりますので、
後は、時々傍らで覗かせて頂くだけにします。
>は間違いであり、正しくは
>6÷(1+2)=6÷((+1)(1+2))=2
>というようになります。
この解説は、9派の論理が間違っているという説明に他ならないよね??
でね!でね!
6÷t を t=1+2=(+1)(1+2) に置き換えた場合、
6÷(1+2) あるいは 6÷((+1)(1+2)) って説明してるじゃん!?
6÷t を t=2(1+2) に置き換えたらどうなる? どうなる??
>「t=(+1)(1+2)」と置き換えたのだから、群論の考え方では、「6÷t」を元に戻すときは
>「1+2」と等しい数にあたる「(+1)(1+2)」を括弧()を用いて「6÷((+1)(1+2))」と戻します。
って書いてるでしょ? 同じ考え方でいくとね!
6÷t を t=2(1+2) に置き換えたら! 6÷(2(1+2)) ってことになるよね!!つまり、
6÷(2(1+2))=1 であり!
6÷2(1+2)=1! ってこと!
6÷2(1+2) の 2(1+2) を t に置き換えるでしょ?
6÷t になるじゃん?
tをもとにもどすじゃん?
6÷(2(1+2))
計算するジャン? =1
おめでとうございますうううう!
残念ながら、群論の考え方をするときは「2(1+2)」全体を
1つの文字tに置き換えている時点で論理的に間違っている。
その証拠にtを元に戻したとき元の式「6÷2(1+2)」は「6÷(2(1+2))」となり、見た目が違っている。
群論で同じことをしたときは元の式「6÷2(1+2)」はそのままであり、見た目も何も変わらない。
いわゆる式の見てくれが変わって来るので、群論の考え方ではその置き換えは間違っている。
群論の考え方をするときは、文字で置き換えてそれを元に戻したとき、
式の見てくれが変わって計算の方法や答えが変わることはあり得ない。
>>2079の1行目の「群論の考え方をするときは」は余計ね。>>2078は最初から義務教育の考え方をしている。
>>2074
私からしたら、群論の最短の学習コースも書いたりして、
答えが9になる考え方については出来る限りのことをしたつもり。
そのように、出来る限りのことはした訳で、
もはや答えが9になる群論の考え方が分からないなら、どうでもいいと思っている。
これ以上頑なに1と考える人を相手にしても、私にとっては時間のムダになって何も意味がない。
そのように感じて来たから、後はどうぞご自由にお書き下さいな。今思うと研究の方に時間を費やすべきだったな。
>>2078は最初から義務教育の考え方をしているからね。
まあ、本当に今思うと頑なに1と考える人を相手にするなら、研究やお勉強の方に時間を使うべきだった。
かなりの時間をムダにしてしまった。私がバカだった。
もしかしたら、人生を台無しにしたのかも知れない。
今となっては後の祭りに過ぎないが、それ位バカなことをした。
簡単にいえば、群論で考えるときは割る数の「2(1+2)」を文字で置き換えるときは、
括弧()内の「1+2」を文字で置き換えないといけないっていうことだ。
まあ、私が書いた>>2069、>>2070、>>2071の内容と比較してみるとよい。
「6÷(1+2)」の「1+2」を文字tで置き換えて「6÷t」として
「6÷t」のtを元に戻しても、「6÷(1+2)」となって元の式のまま。
>>2078の考え方では、そのあたりが違う。
群論の考え方と義務教育の考え方との違いは、文字tで置き換えてtを元に戻しても、元の式のままであるかどうかね。
まあ、私も時間がないのでそれじゃあね。
今となっては後の祭りに過ぎないが、それ位バカなことをした。私も酷いことをしたと思っている。
一応、群論の考え方でも、原理的には「6÷2(1+2)」の「2(1+2)」を
文字tでt=2(1+2)と置き換えることは出来るが、
÷と省略された×との優先順位は等しいから、そのように置き換えたときは
t=2(1+2)=(+2)(+3)などとして省略された掛け算の計算をすることは出来ず、
t=2(1+2)=(+2)(+3)を元に戻すときは括弧()を付けずに
「6÷(+2)(+3)」などとして元に戻さないといけない。
つまり「2(1+2)」を文字で置き換えてその数6を勝手に求めることは出来ない。
そのようなことをすると論理的な破綻が生じる。
まあ、これは補足です。いい加減時間がなくなってきたのでそれでは。後はご自由に。
ここの人のいってる ぐんろん と、ぜんぜん違うもののような気がするんだけど!気のせいかな!?
つまりその考え方からいくと、
6÷(1+2)=6÷1×(1+2)=18
は合ってるってことなんだよ。
だから9になる論理がおかしい。
群論を言い訳に使うなよ。
この条件でaが1の時と2の時で計算方法がかわるわけないだろ!
>>2087
群論の考え方では、「6÷(1+2)」をt=1+2と置き換えたときは、足し算の計算を
割り算より優先させるために括弧()で括られた「1+2」をtで置き換え、1を掛けて1+2=(+1)(1+2)と変形しており、割り算と省略された「×」の計算を同じ優先順位で計算する必要があるから
置き換えたtを元に戻すときは括弧()を補足して「6÷(1+2)=6((+1)(1+2))」とする必要があることに対し、
「6÷2(1+2)」の割る数を「t=2(1+2)」と置き換えたときは、省略された「×」の計算を
割り算と同じ優先順位で計算するから置き換えたtを元に戻すとき、
計算を優先させる意味で付ける括弧()で括る必要はなく、
「6÷2(1+2)=6÷(2(1+2))」として元に戻すことは出来ない。
というか、こんなことを頑なに答えが1と考えている人に書いても意味がないんだろうな。
私は「群論」という言葉を広い意味での群論として使っていた。
正確にいえば、「体の理論」といった方が妥当でしょうね。
体の理論になると「(+6)(+2)^{-1}(1+2)」や「(+6)((+2)(1+2))^{-1}」の類の式に対して、
分配則を用いた計算や、括弧()内を優先させるようにする計算を行う。
体ではどちらの計算もすることも出来て、計算結果は等しくなる。
で、体は通常の加法(いわゆる足し算)について群の構造をもつと同時に
体から0を除いた数の集合は通常の乗法(いわゆる掛け算)についても群の構造を持つから、
体は足し算についても掛け算についても群になる。
そのように考えると、体の理論ましてや数の計算をするときは群論の考え方で計算をすることになり、
特別な体の理論の小難しい知識は必要ないから、その類の計算を「群論の考え方」での計算といっていた。
(続きね)
線型代数も、線型空間は通常の加法(いわゆる足し算)について群だから、
或る意味では群論(可換群の理論)の話になる。
このように、単純に群論といっても、
リー群論や位相群論、有限群論、可換群論、代数群論、表現論など、
幾つかの分野がある。で、群の構造は多くの数学の対象に入っている。
一応ね、「(+6)(+2)^{-1}(1+2)」という式は義務教育風の書き方で書くと「6÷2×(1+2)」、
「(+6)((+2)(1+2))^{-1}」という式は「6÷(2(1+2))」になるからね。
群論と表現論は微妙に違うんだけど、群論で表現が出て来て表現論の話になることもあるから、
群論と表現論とは密接にかかわっている。
まあ、そういうことに興味があるなら、群論を勉強してね。
ガロアという人が作った理論なんて群論の応用だよ。
まあ、こんなことを頑なに答えが1と考えている人に書いても、殆ど何も意味がないんでしょうけどね。
いつまでも頑なに答えが1と考えている人を相手にしている暇はないから、それじゃあね。
もはや頑なに答えが1と考えている人に群論の考え方をいくら説明しても、分からないんだろうなと思っている。
私もこの種の人を相手していてバカバカしいと感じて来たよ。
違う意見を排除する考え方をするような人を相手しても、何の意味もない。
頑なに答えが1と考えている人は、典型的なその種の人なのだとは思う。
{÷と省略された×との優先順位は等しいから}
これって普通の教育だと省略×が優先と思うが群論ではそうなの?
このルールは群論にあるんかね、パッと見載ってない。
実のところ、群論にそういう特殊的な解釈の仕方なんてないんですよ笑
群論君が群論をそういうものだと勘違いしてるだけで…w
(>>2100の続き)
これら(>>2099や>>2100)のようなことが出来るから、「6÷2(1+2)」という式は
表記がおかしいか、答えがあるなら9といっていた訳です。
(>>2101の続き)
群論で考えたとき、勝手に「6÷2(1+2)=6÷(2×1+2×2)=6÷(2+4)=6÷6=1」などという計算は出来ません。
「÷」(つまり「○」)と「×」(つまり「・」)、省略された×の計算の優先順位が定義上は等しい
という原則に反し、同じ優先順位の記号や省略された×で表されているような式を、
勝手に優先順位を変えて計算しているんです。
つまり、>>2083のように論理的な破たんが生じる計算をしているんです。
まあ、「6÷2(1+2)=6÷2[1+2]」などと「2(1+2)」が線型空間の式を表すと仮定されているなら出来ますけど。
しかし、普通に考えれば、「6÷2(1+2)」の括弧()は「+」より「2(1+2)」の省略された×を
優先させて計算する意味で使っている括弧()と解釈するでしょうね。
某サイトで議論したときも同じようなことを書きました。
そこで叩かれていた、文科省に実際に聞いた人によると
「6÷2(1+2)」のような式は書かない、というのは多分事実なんでしょうね。
私自身、そのような「6÷2(1+2)」にとてもよく似た式を義務教育で見て解いた記憶はないんですよね。
もし解いていれば、一々割り算の再定義なんていうバカなことはせずに、答えが1と即答するでしょうね。
>>2099、>>2100、>>2101のようなことをすれば、>>2096のような話になります。
>>2095
補足ですが、私には高度な知識などありません。私より高度な知識があるお方は沢山います。
私は出来損ないのバカ以外の何者でもありません。
そもそも、
>省略された×
という考え方がおかしくて、 2(1+2) の 2 と ( の間に × なんて存在しないんですよ、すでに。
すでに掛けられている状態なわけですから。 なので、優先順位は÷と等しいわけではなく、最優先だと考えたほうがいいかと思います。
まあ、何れにしろ私より高度な知識を持った優秀な人は沢山いる。
今までいっていた群論の考え方での「÷」の再構成というのは、
>>2099、>>2100、>>2101のようなことです。
沢山の人が見ると、話が分からなくなりかねないから書かなかったけど。
まあ、もし分からなかったら、許してね。
「すでに」という言葉を使っているところからすると、
2099、>>2100、>>2101のようなことを時間経過をたどって物理的に考えているようだけど、
>>2099、>>2100、>>2101のようなことを考えるときは、時間経過をたどることはしない方がいい。
「=」の左辺と右辺は等しい。そして=の左辺と右辺を入れ替えることは可能。
だから、「=」で結ばれた式を考えるにあたり「既に」という言葉は数学的には必要ない。
物理的に考えるなら話は別かも知れない。
中学の参考書みてこいよ
その類の式の割る算ならためらいなく計算出来る。
問題は、割る数が「2(1+2)」によく似た式だとどうなるんでしょう、ってこと。
義務教育で考えるとその類の式は、数学的には>>2109の下の部分の考え方を許すようなことをしている。
数学的には、0で割ることが定義出来ることになるという不思議なことが起こる。
「見る様々な意味での余裕はない」は、「様々な意味で見る余裕はない」と訂正。
捏造で記号の優先順位をでっちあげたのは事実。
>>2115
代数は有限性を伴い、代数的な考え方が非可算無限個の実数に対して必ずしも通用するとは限らないから、
この定義の仕方だと、残念ながら一般の実数になると、通用するかどうかが怪しくなる。
私は一般の実数についても通用するような定義をして再構成している。
で、群の作用と同時に体の作用を考えることも原理的には出来る。
>0で割ることが定義出来ることに ナ リ マ セ ン
そのようなことが起こるから、0を除外して普通は群の作用を考える。
そうすると、>>2099のような考え方が出来る。
体の作用を考えて>>2109のようなことは普通は考えない。
テキスト見て例を作っているだけだよ。
元々が「÷」は出来損ないの記号だから、別に義務教育を頑なに否定する気はない。
答えは1ね、1。
数学的には、原理的には9でも1でもどっちでもいいんだけどね。
>本当に、日本で「6÷2(1+2)」にとてもよく似た問題自体が問題として出題された例はあるのか?
>仮に出題された例がないなら、答えが1という主張は怪しくなる。
なんだ さんざんソースを否定しておいて、今度はソースを求めるのかよw
頑なに答えが1とばかり主張している割にはソースが出せないないようではお互い様でしょうと。
私についても同様で、そもそも問題の表記がおかしいが、答えがあるなら9、といっている割には
ソースが出せないようではお互い様でしょうとなる。
つまり、結局は五十歩百歩。
「6÷2(1+2)」という式の括弧()内は3に等しく、式に出て来る数は2、3、6というどれも小学校で出て来る数で、
「6÷2(1+2)」が出て来るとしたら、丁度小学と中学の境目になる。
もしかしたら「6÷2(1+2)」は「6÷2×(1+2)」の書き間違いだったという可能性は否定出来ない。
なんとか引き分けに持ち込もうとしてるwww
群論の考え方をして例を作れば、何か特別な要素がない限り、本来は正しくなるよ。
ましてや、「×」とか「÷」の場合はそう。
ただ、商体を用いて分数などが構成されるという話はある。
私は敢えてそれを無視して「×」や「÷」を再構成した。
その方が義務教育での定義の方法に適っていると思った。
そうですね。
義務教育に合わせて再構成した筈の定義が、かえって話を複雑にしてしまいました。
私も、議論する動機が低くなって来たので、「6÷2(1+2)」について書くことを控えさせて頂きます。
>義務教育に合わせて再構成した筈の定義が
を
>義務教育に合わせて再構成した筈の「こと」が
と訂正させて頂きます。
議論する気がもはやなくなって来たので、「6÷2(1+2)」についての書き込みは控えます。
必ずかきこむくせに・・
群論の問題がおかしい発言は却下!
散々その式を別の式や数に=で結んでいたくせに(要は正しいと認めてる)
都合が悪くなると今度は式が悪い。典型的な9派です。
1派のソースは公式や決まりでしょ。ちなみに群論は公式の使い方ではなく
存在、あり方、使用自体を否定したことも忘れずに。
それをニコニコはソースなんとか主義とか言って完全否定してたくせに・・。
あげくに書き違いだった可能性・・それを必死で群論で説明してたんだろうが・・
義務教育はくだらないとか相手しないとか義務教育を否定することを言ってて
今度は義務教育での定義の方法に適っていると思った。
もうどうにもならんね。病気かよ。
ソース付で!
私自身としてはあるべき姿を追究していたつもりだったんですが、
公式の存在、あり方、使用自体を否定したことはお詫びします。
「6÷2(1+2)」と書かれると、多項式(の係数)としての「1+2」を指し
割る数「2(1+2)」は「2と単項式1+2」とでもいうのでしょうけど、
「1+2」という式については式自体が(小学の)足し算としての「1+2」と捉えることも出来るので、
単純に勝手に「6÷2(1+2)」を中学の計算と決め付ける訳ことにはためらいがあります。
「6÷2(1+2)」が「6÷2×(1+2)」の書き間違いだった可能性は、否定出来ません。
「6÷2(1-4)」なら中学の計算だと判断することは出来ますけど。
「2(1+2)」という式は代数で出て来ます。(高校以降の)解析でも同じです。
ただ、中学では割る数として「2(1+2)」にとてもよく似た式を見た覚えはありません。
(続き)
「6÷2(1+2)」という式は括弧()内の計算が小学の計算で答えが3で2、3、6が小学で出て来る数であり、
義務教育の知識で「6÷2(1+2)」を、単純に中学の問題なのか
小学の問題の書き間違いだったのか、判断して計算することは何かためらいを感じて不可能です。
あと、>>2129の
>割る数「2(1+2)」は「2と単項式1+2」とでもいうのでしょうけど、
は
>割る数「2(1+2)」は「2と単項式1+2との積」とでもいうのでしょうけど、
の間違いです。
>割る数「2(1+2)」は「2と単項式1+2」とでもいうのでしょうけど、
は
>割る数「2(1+2)」は「2と単項式1+2との掛け算の答え」とでもいうのでしょうけど、
の間違いです。
などとでもした方がよいのかも知れません。
私は殆どアドリブで考えて書いていて、
書いた内容の全体的な流れをたどると矛盾が生じていますが、
そこはご勘弁下さい。
(今まで)本気モードになって(群論で)「×」「÷」を再構成していた訳ではありません。
再構成した内容を書いた代物はありません。
敢えて再構成するとしたら、これまで書いたようになるのではないかと。
むしろ頑なに答えが1と主張している人の方がソースを出すべきではないのかと。
私のような場合は単なる戯言に過ぎず、現実的にはソース自体の現実的直接的提示は不可能なのですが、
頑なに答えが1と主張している人の場合は、
「6÷2(1+2)」にとてもよく似た式自体が計算問題として出された例のようだと、
その例は物理的に現実に存在する(存在した)ことになりますので。
少しまとまった時間がほしいので、「6÷2(1+2)」についてこれ以上は書くことは控えます。
安い魚だ
>>2136
>>2137
釣りだか魚だか何だか知りませんけど、「6÷2(1+2)」について
いつまでも掲示板で書いて議論している暇はありません。
私には、行うにはかなりまとまった時間が必要で、
かつ紙に書かないと出来ないようなことがあるので、さようなら
まあ、釣りだの魚だのということは、某サイトのし過ぎでしょうね
(少なくとも1週間以上必要な(手)計算(解析)をしたことなどないんだろうな。
こういうのは、失敗したらムダに終わりかねないがうまくいったら感激モノだよ)。
>かつ紙に書かないと出来ないようなことがあるので、さようなら
の部分では句読点「。」を付けることを忘れたな。
ただの見てくれに過ぎず、本質は変わらないのだが。
まあ、マジメに紙に書いてまとめるべきことがあるので、「6÷2(1+2)」について、後はもう知らん。
釣りでも何でもご自由に。
お疲れ様でした。6÷2(1+2)について、群、環、体、その他、分数を表す商体など、沢山学ばせていただきました。数学の表現は、まじめに考えると、÷という記号は使わず、例えば、67≡13 (mod 18)と表現できるとか。商体だと、分数を、より正確に表すものだということもわかりました(ほんと、法律用語みたいに、がちがちですね。だから、本当は再定義したほうが、表現としてより正確になるという反面、難しくなるというジレンマがあると思います。)
私自身、割るという記号は、もうほとんど見ることがなくなり、更に、自分から使うことはなくなりました。割る数があいまいという理由で。電卓の÷の記号使うときに、注意するくらいかな。数学って、誰かから与えられた公式を使って考えても、あまり意味ありませんね。そこで議論がストップしてしまうから。演算子について、いろいろ考えさせられました。
最後に、めんどくさい人が沢山いるので、答えは1にしておきます。
これはオレが釣られているのか??
ものすごく自作自演臭がするんだけど…
>実際は一人。
ニコニコにも同一人物が書き込んでいる可能性大。
>両者が省略された積という言葉を使い訂正が同じく多い。
群論を語る人間は複数いる。
>実際は一人。ソースは?ソースがないと、ただの妄想です。これがあなた方の言い分ですね。
反論できないからって、捨て台詞か。はい論破www
それ群論ジャン!?2138、2139、2142とかまさにそれ。
本当にすぐに食いつくな。
(この文自体が確かであるという証拠など、どこにもないが)。
私が>>2142などと同一人物に見えたりすることは、
書いた時間帯や「>>」を用いて書いている点などが似ていることから同一人物に見える
という、或る種の思い込みだよ。
何も確固たる根拠はなく、ただの勝手な判断に過ぎない。
>>2141が誰あてなのか判断しかねますけど、人の判断に学歴なんて余りあてになりませんけどね。
しかし釣りだかの数が多いな。
まあ、下らんことはしない方がいいだろうな。
そういうことをしても意味がない。
まあ、お仕事の続きするけど。
うん、群論も自分の間違いを認めたみたい
>>2152
結論は9だよ。はい、つれた
釣り文句はどの文?
本来は分数など用いる必要などなく、>>2099を一部変えて、実数体R上の二項演算
・:R×R∋(a、b)→a・b∈R、 a・b=ab
を考えることで通常の掛け算の記号「×」(つまり「・」)を再定義したり
体Rの乗法群R^{×}の、Rへの右作用
○:R×R^{×}∋(a、b)→a○b∈R、 a○b=a・b^{-1}=ab^{-1}
を考えることによって、通常の割り算の記号「÷」(つまり「○」)を再定義したりすれば、「6÷2(1+2)」は等位で
6÷2(1+2)=(+6)÷(+2)(1+2)=(+6)÷(+2)(+3)=(+6)÷(+2)×(+3)
=(+6)○(+2)・(+3)=(+6)(+2)^{-1}(+3)
=(+6)・(+2)^{-1}・(+3)=6・2^{-1}・3=9
とでも計算出来る。
公式は守らないのに正しい日本語は守れと言うからな群論は
私のような場合は単なる戯言に過ぎず、現実的にはソース自体の現実的直接的提示は不可能
私のような場合は単なる戯言に過ぎず、現実的にはソース自体の現実的直接的提示は不可能
私のような場合は単なる戯言に過ぎず、現実的にはソース自体の現実的直接的提示は不可能
いつまでも戯言言ってないで(嘘の)仕事に戻れ
だから群論しなくていいんだってw
普通は商体で分数を定義するから、私のように群論で分数を考えるようなことはしないけど。
一応、試しに思考実験しているだけ。
でね、>>2169のような考え方をすると、
2 2 2 3
6÷(――)=6÷(+――)=6・(+――)^{-1}=6・(+――)=6・(3÷2)=6・(3・2^{-1})=6・3・2^{-1}=9
3 3 3 2
とでも考えて等位で計算出来ると思うんだよね。2を√2に置き換えても同様。
これは単なる思考実験で、考えがまとまった代物などないんだけどね。
まあ、分かりにくかったら、「・」は「×」に置き換えて読んでね。
うまく分母と分子をずらして読んでほしい。
まあ、お仕事の続きだ。
もし書くとしたら、明日以降。
私は同様の式は文字を含む式なら見たことはあります。
ただ数字だけだと問題はないですね。解答には2・3の様な表記はありました。
これの表記についてですが、2(1+2) この書き方はいいのか悪いのか。
良ければ当然答えは1になります。
悪ければ、式が間違っているになります。解答不能。
なので修正するとして×を加えて初めて9という答えが出てきます。
ただ修正の仕方は複数存在するので、修正案の中の1つが初めて9になります。
6÷2×(1+2)
6÷{2×(1+2)}
なので6÷2(1+2)からは1か問題が間違いしか生まれません。
これは1派と不備派の争いだったのですが()含む数字のみの×の省略は可能か?になります。
不備派は可能とする1派に対し、使用例のあるサイトを求めました。悪魔の証明っていう奴です。
無いのは証明できないからあるという側が証明すべき。
という声が広がり問題が悪いという結論になりかけました。
しかし数か月前から1派のソースとして有名なニコニコ大百科で結論は1となりました。
そこには当然、数字のみの式で×を省略していたサイトが複数ありました。
これによって形勢は一気に1派有利に傾きました。
使用例はあるが使用してはいけないというソースは未だ見つかっていません。
はっきりした結論は出ていませんが、どこも1派が有利なのは変わらないようです。
1派の人に9だといったら、過敏に反応するから、それが正解だと誰も言ってないのに。答えを1にしたくて必死な感じがwwww
有利なだけ。6÷2(1+2)を計算せよで、答えが1というソース。ニコニコのふわっとしたソースでなくて。
ニコニコの中で答えが1に決まっただけ。実際は、何も決まってない。なのに1が正しいと言い張るのがおかしくて…。答えが1に決まったソース出せ。
勝手に自分たち専用の場所だと思い込み
他者を余所者だと決め付けて排斥する。
本質はこれだろ
そもそも何も決まってない
群論の下僕が今更何言ってんの?つうか同一人物だろ。
一部の特化した連中?義務教育上は1なんだよ。それは認めてるわな。
特化した連中は群論のことでしょ。そもそも群論の使用法自体を間違ってるし。
群論自体が1でいいと書いているんだよ。他に9派はいないだろ。
あとな、別人を装って書くと余計に不自然になる場合がある。wwや改行をしない、口調を変える。
一行の長さを変える。言ってる内容は同じ。
そもそも群論自体を悪用して自己主張したんだからその位軽いわな。ただもっとうまくやれよ。
証拠がないからね。だからIDがあり、正確な議論をするルールがあるニコニコで書き込めないわけだ。
あと本気でニコニコがソースとでも思ってるのか?ソースが集められてんだよ。
つうかじゃあ、9のソースを出せよ!と言ったら出せるのかよ。そもそも群論で主張する奴が逆方向に特化
していると気づけよ。
勝手に自分たち専用の場所だと思い込み
他者を余所者だと決め付けて排斥する。
本質はこれだろ
言い方は悪いが、議論なんてそんなもんだよ。
会社の会議やプレゼンなんてそんなもの。当然、他者の支持を多く得た者が勝つ。
逆になあなあで終わればやる意味がない。
私が書いた>>2169~>>2172の趣旨が分からないのなら、別にそれでいい。
>>2183
>特化した連中は群論のことでしょ。そもそも群論の使用法自体を間違ってるし。
少なくとも分数の部分を除いては、群論の使用方法は正しいね。
分数の部分だと私も正しいという絶対的確信があるとはいえないが。
>そもそも群論自体を悪用して自己主張したんだからその位軽いわな。
あらあら~、こんなことを書いちゃったらダメだよ。
(続き)
>>2181の
>そもそも何も決まってない
は、現状では正しい見解だよ。
何せ、頑なに答えが1と主張する割りには、「6÷2(1+2)」にとてもよく似た
問題自体が計算問題として日本の義務教育で出されたという、
物理的に存在する(存在した)ソースが出せないようだからね。
で、6÷2(1+2)を計算せよで、答えが1というソースは?想像で物言っちゃだめだよ。
きみこそ、ニコニコの下僕だろ。だから、ニコニコの中で答えは1っていってるじゃん。
9のソースをよろしく!!
あれ?ここで議論してるのにそもそもなんでニコニコが出てくるの?よそはよそ、うちはうち。
それ、何の議論?いうことなくなったら、それだね。つられてやんの
効いてる効いてる♪
で、6÷2(1+2)を計算せよで、答えが1というソースは?
何も決まってないのに効いてるとか。
お分かり??
ニコニコはただソースがまとめられてるだけ。
なぜニコニコに拒絶反応示すの?
そんなのどうでもいいから、6÷2(1+2)を計算せよで、答えが1というソースだせ?
下僕はバカか?1のソースなんて何個もあるんだよ。
ニコニコ大百科をみましょうね!
で9のソースは??是非知りたい!!早く早く!!
>>2191
私=>>2187については、>>2195の仰る通りだよ。
上手く行けば金もらえるかも知れんぞ
何この必死なかんじ。つられてやんの
以前散々、掛け算や割り算を群論で再構成することを試みるために必要なソースは出した。
後は、内容を理解して再構成あるのみ。
それを書いた代物は、>>2157に書いた。
で、答えが1のソースは?言い訳はいいから。
>>2205では
>以前散々、掛け算や割り算を群論で再構成することを試みるために必要なソースは出した。
の部分の「ソース」は、本来は「テキスト」や「参考書」とでもいう言葉だ。
だが、ソース信者にとっては「ソース」で通用するだろう。
ソースは情報源だよ?君のはただの意見だよ?
早く早く!ソースはよはよ!!
あと勝手に群論に絡んでるけど何がしたいの?
グーグルには指摘できないんだね。反論できることは反論するのに、答えが1のソースは?は9のソース出せしかいえないんだね。相変わらずの議論だ。
それ問題になった源じゃん。問題の元を引っ張り出して何がしたいわけ?
じゃ早く9のソース出せよ!
批判は、俺じゃなく、ソース元へどうぞ
でもそれ、義務教育では違いが生じる不完全なモノだったんだろ。
結局群論と義務教育では違いが生ずると書いたのは無く、個人の意見だったよな。
早く違いが生ずるソースを出せ
下僕はバカか?だからその記事が元になってここまで議論が大きくなったんだろ?
その元を持ってきて9とか・・アスぺもここまでいくとすさまじいな。
群論やテキストや参考書を読んで、義務教育に合わせて具体例を(再)構成するだけ。
殆どそれあるのみ。
掛け算や割り算が、足し算や引き算より優先されることを知っていれば、再構成は出来る。
>>2157は、そうするといえるような1つのこと。
でた。人に、ソース攻めする人。君こそ、納得のいくソース出してみろよ。人に時間取らせておいて、出したらだんまり。
反論できてませんwwww
1信者乙!きんもー☆
ニコニコにあるよ。下僕自身が見ればいい。早く下僕もソースを出せよ。
アスぺは頭が悪いな。知恵遅れの下僕は。
2(1+2)を実数体Rの1つの元と見なすと、2(1+2)≠0なんだから、
「6÷2(1+2)=6÷(2(1+2))」と考えることが出来るし、
2(1+2)を実数体Rの1つの元と見なさないのなら、
「6÷2(1+2)=6÷2×(1+2)」と考えることも出来る。
割る数の「2(1+2)」については、論理的には括弧()内を先に計算しないと不備が起こるから、
私は>>2157のように「6÷2(1+2)=6÷2×(1+2)」と考えている。
「2(1+2)」全体を割る数と見なすなら、括弧()内を文字で置き換えて
0でないことを確認する操作をしなと、論理的に手順前後が生じる。
ちゃんとしたのだったら大百科にのるかもよ?大嫌いなニコニコの。
その考えが公式に反してしまう点についての考えは?
基本的には、論理的に不備が生じないならそれでよいという立場。
まあ、「6÷2(1+2)」については、原理的には割る数の「2(1+2)」の
括弧()内を文字で置き換えて計算することも出来るし、
例の>>2157のように「6÷2(1+2)=6÷2×(1+2)」と考えることも出来るから、
「式の書き方がおかしい」が妥当でしょうね。
仮に答えがあるなら、9とした方が妥当でしょうね。
「6÷2(1+2)=6÷(2(1+2))」と考えるなら、確かに割る数について「2(1+2)≠0」はすぐ分かりますけど、
そういう式を書くと、何で解析をしている訳でもないのに、
割る数「2(1+2)」の括弧()内を先に計算していないのに
「2(1+2)≠0」がすぐ分かるのか、という疑問が生じますね。
「6÷2(1+2)」に答えがあるなら、出来るだけ代数的に考えるべきでしょうね。
そういう考えは間違ってるんだよね。現代数学では。特殊な思考の持ち主もいるもんだ。
例えば、「6÷2(1+2)」の形に似た式
6÷2(1+2+2+3+6-2-1-3-5-2+1+2+6+2-8-3)
だったりすると、「6÷2(1+2)」で「6÷2(1+2)=6÷(2(1+2))」と考えたときと同様に、単純に
6÷2(1+2+2+3+6-2-1-3-5-2+1+2+6+2-8-3)=6÷(2(1+2+2+3+6-2-1-3-5-2+1+2+6+2-8-3))
とでも考えられますか、っていう話になるとは思いますね。
このようなときは、割る数「2(1+2+2+3+6-2-1-3-5-2+1+2+6+2-8-3)」を文字で置き換えて計算して
括弧()内が0でないことを確認する方が最初でしょうね。
そういうようなこともあります。
何かまとまった文章になってはいませんが、>>2232、>>2233、>>2235が一連の見解だと思って下さい。
>>2235のように、割る数の括弧()内が簡単に計算出来るような式であり、
かつその括弧()内の式が複雑になればなる程、
単純に公式が通用するとは限らなくなるとは思います。
???????????????????????????・・
>>2235の
>割る数「2(1+2+2+3+6-2-1-3-5-2+1+2+6+2-8-3)」を文字で置き換えて計算して
の部分は、
>割る数の括弧()内「1+2+2+3+6-2-1-3-5-2+1+2+6+2-8-3」を文字で置き換えて計算して
の間違いです。
すみません。
>>2235は、答えがあるとして公式絶対主義の人(頑なに答えが1という人)向けに書いたような文章だよ。
まあ、正確には
6÷2(1+2+2+3+6-2-1-3-5-2+1+2+6+2-8-1)
とした方が括弧()内が「1+2=3」に等しくなって、「6÷2(1+2)」に形が似た式になるけど。
こういう式になると、括弧()内が0になる可能性があるから、
単純に公式が使えるとは限らないでしょうね。
同じ答えを1と求めるにしても、括弧()内の置き換えではなく公式を使ったら
論理的に不備がある計算をしていることになる。
そもそも割る数が0ではないなんてわかってるよ。
割る数が0だったらみんな式が間違いって言うわ。
公式は間違ってるとか言って、今度は使えるとは限らない・・
本当にその場その場でごくろーちゃんです。
>そもそも割る数が0ではないなんてわかってるよ。
そう仮定している時点で、論理的に不備が生じるような計算をしている。
論理的には割る数が0になることの確認が先で、割ることをするのはその後。
こういうことは、別に群論をしていなくても、
マトモな微積分をしたことがある人なら分かるような感覚のことだよ。
果たして本当に割ることが出来るのかどうかとかね。
にこにこにのって、なんかすごいの?別にたいしたことないじゃん。にこにこがちゃんとしたものとかwwwwwww
6÷2(1+2)を計算せよで、答えが1というソースをここにだせ。
>別に群論をしていなくても、
の部分は
>別に群論を「知らなく」ても、
と訂正。
まあ、微積分でε-δなどをしたことがあるなら、>>2241のようなことは分かるな。
0で割ってはいけません、っていうことが身にしみる。
高校数学の微積分だと怪しいかも知れない。
6÷2(1+2)=? 百萬人錯答「1」のいみがわかんない?訳すと、おもいっきり、100万人が間違った答え1ってかいてある。思いっきり、ど直球なソースだが。で、それは否定できているの?
ソース出したら、それは違うってじゃあ、違うって言うソース出せ。にこにこにしかないんでしょ。それも、誰かわからん人の教科書とかwwww。
だいたい※2235なにあれ?
今までで最高に意味がわからなかったんだけど。
いよいよ壊れたのかな?って思うレベル。
※2235はっきり言って読むのも嫌になって読んでいません。
本当に壊れた??あ、2235のことね。
なら、それを学会で発表したら?
それに、6÷2(1+2)=? 百萬人錯答「1」じたいは否定できてませんね。
結局何も決まってないのに、答えを1にしたがるとか。
でた、典型的だね。それ本当に正しいの?
ソースつきでいいたいことあるなら、にこにこでしたら?なんでここ?
何かあったのか?
じゃあ、それを世間に認めさせたら。少なくとも、あなたたちが勝手にやってる茶番の理論ですよね。ニコニコで、茶番の理論展開してるじゃん。どっかの算数ドリルの一説とか抜き出して。学会にはとても恥ずかしくて、載せられないような内容ばかりだ。
いやいや、そもそもこのちんけな話題を学会とかで発表するってどういう発想なの?
軍論氏が多くの人から学会で発表しろだの言われていたのは、「群論?で新しい体系を構築するような話をしていたから」でしょ笑 大きな風呂敷を広げたあなたこそが、自身の持論をもって、学会に殴りこむべきなんですよ。
6÷2(1+2)=1 は、一般常識
6÷2(1+2)=9 は、世界の数学学会を揺るがす新発想
さあ、こんなところに書き込んでる時間はない。立派な論文をまとめて、フィールズ賞を目指してください!
6÷2() の()内の足し算引き算が増えれば増えるほど数学的に不安定な式になる的なよくわからない話してたけど、普通に計算するだけだよ。結果、(0)なら割っちゃいけないだけの話ですね。みんな※2235の話の内容がお粗末過ぎて絶句してたね。
元から変だとは思ってたけど・・。
ちなみに1派の計算問題は全部正しいよな。
とりあえず2249見ろ・・
世間はとっくに認められてるわけで・・教育課程に含まれてるよ。
一部わけのわからない思想を持ったのがいるわけでね。
いろいろ出されておかしくなったのか?
ちなみに9派もソース何か出せよな・・
お前がソース出せとか言ったんじゃないの?
何か変な奴が多いな
は?1でも9でも、とくにたいしたことないじゃん。フィールズ賞?ばかじゃないの?
ニコニコのソースここで出して何の議論したいの?にこにこですれば?あらしにきたの?
1が一般常識とか。おかしすぎる。がんばって1という答えが一般常識になったらいいね。そんなに認めさせたいのか。街頭で、宣伝でもしてください。
答えが1 ふーん、そうなんだ。
答えが9 ふーん、そうなんだ。
何が一般常識だよ。ちゃんちゃらおかしい
少し忙しく、それ以降は何も書いていなかった
(これのソースなどどこにもないが)。
これ以降も忙しくて、必ずしも見る暇があるとは限らない。
例え見たとしても、多分書かないだろう
(>>2265の文章を見て、もはや議論してもムダだと悟った)。
ファビョってる人=群論=2283
必死に話題を反らそうとしてるな。
素敵な同志が湧いてきてくれてよかったですね!
問題や考えること自体を批判しはじめたか。末期だな。
1に固執してるのはどっちだい?ニコニコの理論持ち出して、一般常識です ( ・`ω・´) !
答えを何が何でも1にしたいんですね。言い続けたら、なるかもしれないよ。
6÷2(1+2)=9 は、世界の数学学会を揺るがす新発想wwwwwwwwwwww
なんだそれ?
9派じゃなく、問題があいまい派だよ。そっちこそ、勝手に私たちの解釈変えんな!
1 (Juice) or (Water with ice)
2 (Juice or Water) with ice
1と2は意味が変わってくるでしょ。
だから、カンマ「,」をうちなさい。
I want like to Juice or Water, with the ice.
これと同じように、あいまいな式を書かないでください
いやいやそれを信じてるのはお前だよ。群論
あと上のキチガイは死ね。
2011年ですので議論された当初の投稿ですね。
不備派にはおおざっぱに2種類あります。
①・・1とも9ともとれるから問題が悪い
②・・数字のみで×を省略はできない
あなたは①ですね。②は※2256で使用例が多数あるので問題なし。
それだけじゃ使っていいと言えないという声もありましたが
逆に使ってはいけないソースが無い為、また教科書にも使用があったので
ほぼこれについては問題はあなくなりました。
1派・・A÷(B×C)
9派・・A÷B×C
不備派・・どっちにもとれる
マジレスするとA÷(B×C)がただしい。
釣りなのか?
6÷2=3だろ?
(1+2)=3だよな?
今の中学生の数式じゃあ、たとえばこの数式に当てはめたら・・・
(1の前に記号が無かったら×を入れるんだ。
この問題は大人がゆとりだってバカにしてる俺たちガキの方が正解率高いんじゃね?
くず、死ねか。とうとう、本性でましたね。そういうこという時点で、人格が破綻している。それで、何を説明するの?信用が0だよ。ま、一人の人格破綻者が持論述べているだけだというのがわかりました。もうこないでください。荒らしでしょ。
海外ではどうか知らないので、日本で通じる数学ということがわかりました。国際ルールでなくて、あくまでローカルルールですね。6÷2(1+2)=1ただし日本に限る。これが正解ということか。意味わからん。
6÷2(1+2)=1 は、一般常識の意味がわかりません。二本での一般常識ですよね。それに、周りに知ってる人が全然いません。特殊な事例ですよね。100歩譲って。
なくなりましたのいみがわからん。勝手に終わらせてるだけでしょ。議論から逃げてるのか。
二本は日本です。まちがえました
問題がなくなりましたとか。勝手に解釈して、問題ないってwwwwwwwww。
6
--(1+2)と書けばいいだけなのに。
2
マジレスするとA÷(B×C)がただしい。
なんだ、ほかは適当に書いたレスなんだ。
なら、信用できません。
ソース付で主張しろよ。
とりあえずここは日本です。日本の決まりがあります。
次の2つ、どう答えますか?
① 6÷2×a
② 6÷2a
これくらいは解けますよね?
ちなみに9派はこれ、同じですよね?
6
--(1+2)と書けばいいだけなのに。 誤
2
6
---- と書けばいいだけなのに。 正
2(1+2)
両方式としては成立しているよ。またじぶんかってな解釈した。両方計算できるのに、間違えとか。意味わからん。
自分は書いた人ではないので2312に答えてください
6÷2(1+2)の÷を省略すれば正の方になります。
誤の式はまったく別の式だよ。
2313よろしく
何で、お前がソースを決めるねん。ソース出せっていったから出したら、自分勝手な解釈。どっちか答えが決まらないから出したのに、何であなたの検閲が必要なの?あなたは、数学の神様なのですか?
もういいよ。そんなせりふは。ま、1を信じてる人は、大体そういう人だっていうのはわかりました。
そもそも、数学の日本の決まりって何ですか?意味わかりません。ひょっとして、日本だけでしか成り立たないってことですか?世界に拡張できない数学wwwwwwww。万国共通じゃないのかよwwwwwwww。そんな、ローカルルールの数学が一般常識とか。これが、答え1のクオリティか。
各ソースはニコニコとは全く関係ない。
日本語話して会話するのは日本人の一般常識だぞ?ん?
ガジェットの海外版、海外の動画あげてますよね?
議論と言いつつ議論から逃げ悪態ばかり。
あとあなたはどこの国の人ですか?
とりあえず2312が都合が悪いので答えたくないのはわかりました。
2326
ニコニコはソースをまとめているだけといいながら、ニコニコからの転載ですね。全然関係ないといいながらまたおかしなこといってる
あーあ、そこまでぼけた?日本語を会話する人=日本人だって。たのむよ。一応、数学勉強してるんでしょ。日本語を会話する人は日本人も外国人もいる。日本人でも、しゃべれない人がいる。例えば声帯がつぶれている人とかね。
日本国で学ぶ国語(学)があなたのおっしゃる意味だとして、数学が、なぜ外国で通用しないんだ。論理が破綻してる。いっぱいあるけど、ピタゴラスの定理(ギリシア)、オイラーの定理(スイス)、まだまだ出てくるけど、それらを使って数学が成り立っていますが。日本の数学って何ですか?
必死だな。そんなに1にしてほしいのかwwwwwww
終わった議論だから、6÷2(1+2)=9ですwwwwwwwwww
あと勝手に話題を反らして議論しないようにする汚物だよお前は。
あと日本の数学が外国で通用しないとどこで書いてある?そんなこと書いてないぞ?ん?
死ね本当に。
※2312
お前はどこの国の人間か?
発言変えただけでお前群論じゃねえか?
都合が悪いのはどっちだよ。早く答えろよ。
本当に頭悪いな
日本語を会話するのは日本人にとって常識だが外人は会話しない、してはいけないと
どこで書いた?
だけど米国だと右側走行が一般常識。
じゃあ日本人は米国で車運転するときは左側走るか?
アメリカ人は日本で右側走るか?
ここは日本の常識で考えるべき。
世界の常識がこの6÷・・・がどうかは知らないけどな。
まともな議論はできそうにもないので。
群論君は終わりましたな
何で、車の運転と数学が同列で語られるかなー。あーあ、ここまでおちたか。ニコニコのソースで、ここにきて、人には質問しておいて、自分は私の提示したソースに答えない。世界は知らんが、日本の数学があることを認め、そして、日本の数学の常識を求める。答えを1にするためにそうせざるをえないんでしょ。もう来ないといいながら、またくるんでしょうね。日本の数学の中で、あなたの中において答え1というのはわかりましたwwwwwwwww
はーい、汚物いただきました。答え1って言う人は、こんなもんですよ。もうこないでください。あらしはよそでやってください。ニコニコの転載に、数々の暴言。そして、人に答えを求めておきながら、自分は却下。しばらく来ないという言葉を一応信じますwwwww。
自分は私の提示したソースに答えない。は、あなたは私の提示したソースに答えないの誤りです。すみません
本当に消えてなくなればいいのに・・発達障害児
休むきないじゃん。また嘘ついたwwwwwwwwww
すべての(相手をバカにする)発言において自分のことを棚上げしてることに気付いてない。
下僕群論
言い訳乙wwwwww。
またボケって言った。なんか、ほんと最低だなwwwwwwww
これで、ニコニコの下僕も納得だね。暴言はくし、嘘つくし、この程度ですよ。まともに議論できるとは思わないwwwwww。また、なんか文句吐きに来て、スレを汚しに来てくださいwwwwwwww
そうすりゃこの議論も終わる。
数学者たちよ頼んだ。
おまえらが画面に向かってムキになりながら書き込んでる姿を想像したらクッソ萎えた
クッソ汚いブサイク共がそんなことしてたらそりゃ引くわー^^
~想像したらクッソ萎えた
1人で妄想して笑って・・・・・
こいつ引きこもりか何かだろ
(s山k)が閃かなくても、閃きに値しないから閃かなくなっただけということは、容易に分かる。
人豚は心汚い。
頭がかたいねぇ
今時の大人は
1.注記を示す カエサル(シーザー)が暗殺され、……
2.補足を示す 小論文(または、研究報告)を提出しなければ、……
3.引用の出典を示す これは「日常会話の隠喩(杉本 2002)」の例である。
4.著作物の刊行年を示す 古大内(1997)によれば、村上春樹の小説では……
1の用法でこの問題を解釈し、
6÷2(1+2)=6÷2(3)=3
答えは「3」っしょ!
だって6÷2と(1+2)の間に記号がないから。
6÷2=3
1+2=3
だからだぜ!
大人たち!小学生を舐めんんなよ!
今耳当て当ててて暑い・・・
どーでもいいや。
3の人いないな!
うちって天才!
受験受かっちゃうかも!
ヤッタゼィ!
一つの数として見ていいのか、それとも6÷2×3と見ていいのか謎だじぇー
6÷2a=2a分の6 であり
a=1+2 を代入し
6÷2(1+2)=2(1+2)分の6 つまり
6÷2(1+2)=1
要するに意味がこんがらがることなければわたしゃそれでいいですわ。
問題つくんないとこうなる
式自体が成立していない
by数学者
URLは載せることができないようにはちま起稿で設定されてるようだから場所を示す
今がチャンス!花道流基礎固め術(テストの花道)
A=6 B=2 C=(1+2) として、
問題の式をA÷BCと捉えると、BCは「積」、つまり一つの集合です。
BCは求められた「結果」を示すモノなので、切り離して処理出来ません。
BCはコレを紐解く際に、B×Cと解析するダケのコトなので、誤ってコレを
A÷B×C
として左から演算してしまうと、BCは集合でなかったことになっちゃいます。
多分この辺りの解釈を誤ってらっしゃるようです。群論さん。
代数aを使った2aは『aがなにかわかんないけど取り合えずそれの二倍』
だから6÷2a≠6÷2×aはokでも、
ここ代数じゃないじゃん。
算数でも数学でも同じ 一貫している
どんなに構成要素が増えようとも一貫している
ここで問題となっているのは()やaの意味
()やaは×という要素を持っているのは
教科書に載っている
ホントは教科書に載っていても載っていなくても
()やaの意味を個人個人決めたらいい
ただその時は意味を説明してくれないと
どう解釈していいか分からない
長々と失礼
簡単すぎ(笑)私、中1です(^O^)/
毎日、電車に揺られて学校へ。
まぁ、そんなことより答えは9ですょ。どう、ちまよったら1になるのかはわかりませんね(大汗)
9ってやつは
2a÷2a を
2×a÷2×a=a^2
っていうのと同じ考えってことやろ?
いままでそうしてきたん?
2a分の2aという表現だとaが分母にくるので従って1になる
表現によってaが分子になったり分母になったりするからこの手の間違いをすることになる
>問題の式をA÷BCと捉えると、BCは「積」、つまり一つの集合です。
>BCは求められた「結果」を示すモノなので、切り離して処理出来ません。
>BCはコレを紐解く際に、B×Cと解析するダケのコトなので、誤ってコレを
>A÷B×C
>として左から演算してしまうと、BCは集合でなかったことになっちゃいます。
あなたは、集合論という、群論以前の数学の基本中の基本を理解していないことが伺える。
ここでいう「集合」は正しくは「元」或いは「要素」、幾何学的に「点」とでもいうべきである。
数学の基本的言葉を混同しているにもかかわらず、
群論による考え方(小学式に律儀に考える方法に近い)を否定することはやめて頂きたい。
(続き)文章などによる何の説明もなくただ「6÷2(1+2)」という式を出されたなら、
数学的には割る数「2(1+2)」で1元と見なす考え方(中学式の考え方)と、
1と1+2を別個に切り離してそれぞれを1元と見なす考え方(体論などの抽象代数の考え方)
が2(1+2)≠0である以上は原理的には可能である。後者の場合の計算式は例えば
6・2^{-1}(1+2)=6・2^{-1}・(1+2)=6・2^{-1}・3=(6・2^{-1})・3=3・3=9
のようになる。小学校の「÷」の定義に従えば、数学的に厳密に考えれば答えがあるなら本来は9になる。
だが、何故か中学でこの点が食い違っているから、前者で考えることも出来てこのときは答えがあるなら1になる。
そのため、「6÷2(1+2)」という式の表記がおかしいのである。
(続き)そもそも、空気を読むなんて芸当は国土が狭く人口が多い日本だから出来るようことであり、
国土が風呂いアメリカやロシアなどの国になると、そのような芸当は出来ないであろう。
そのため、「6÷2(1+2)=1」などというかなり空気を読んだような方法でありあうんの呼吸でするような、
かなり空気を読んだ上で計算することは、数学をするうえでは極力避けるべきである。
>>2397のはじめの式は正確には「6÷2(1+2)=6・2^{-1}(1+2)」である。
体論のテキストには、「体とは加減乗除が自由に出来るような代数系である云々」と書いてあるから、
通常の乗法は通常の加法より優先させるというごくごく当たり前のことを
知っていれば、>>2397のような計算は出来る。答えを9とする考え方は、それに基づいて計算しているだけである。
(続き)尚、>>2387のいう「代数学」は、普通の人はやらない環や体などの抽象代数を指すと思われる。
一応>>2398の下から3行目の「体論のテキスト」は「体論の大抵のテキスト」と訂正。
というか、抽象代数を知らずに、群論の考え方を否定して、議論をけしかけるようなことはやめてくれよ…。
日本の教育を踏まえて考えると、答えがあるなら1なる。
ただ、数学的には厳密には答えは1ではなく本来は9になる。
そのため、式の書き方がおかしい。
「÷」の機能が小学と中学で異なっている。「÷」を群論で再構成してみて分かった。
「6÷2(1+2)」は、文章による説明が全くないから、式がおかしいで終了。
今気付いたが、>>2398の上から2行目の
>国土が風呂いアメリカやロシアなどの国になると
は、
>国土が「広い」アメリカやロシアなどの国になると
の間違い。「ひろい(hiroi)」とタイプして変換したつもりが、
無意識のうちに「ふろい(huroi)」とタイプしていたみたい。
「u」と「i」のキーが隣にあるから無意識にしていたのかも知れない。
あと、>>2397の
>1と1+2を別個に切り離してそれぞれを1元と見なす考え方(体論などの抽象代数の考え方)
は
>「2」と1+2を別個に切り離してそれぞれを1元と見なす考え方(体論などの抽象代数の考え方)
の間違い(訂正出来る人は、これ位は文脈から訂正して読めるとは思うが)。
うん。だってさ、余弦定理をcosθ= の形にした奴だって
÷2bcしてるけどこれを÷2×b×cにはしないでしょ
やっぱさ、人は自然と×を省略するものを先に計算するんだよ。
厳密には、「6÷2(1+2)」の割る数「2(1+2)」のような省略された掛け算でも()内に足し算があり
()内が計算出来るときは、本来は「÷」よりそれを第一に優先させる。
変な例かも知れないが、「銭湯ではきものを脱ぎましょう」という文は
(1)、銭湯で履物を脱ぎましょう
(2)、銭湯では着物を脱ぎましょう
の2通りに解釈出来て意味が場面によって異なるじゃないか。その文だけでは意味は曖昧だろ。
それと同じような曖昧さが「6÷2(1+2)」という式にはあるんだよ。だから、式がおかしいという訳。
大きな仕事があるからくだらないことはやってられない
とか言って逃げ出したのにね。ソースも1つも示せず。
一般の教育や公式をを否定して優越感に浸ってる変な人だから。
相手してるとおかしくなるよ。
数コメあとには訂正。かわらないね~
中学の教育は間違ってる!文部省や教育機関の文句。
公式を言うとなぜか怒る。群論を誇らしげに語るが
平行の定義すら理解できておらず、球体表面上に直線を
上から下まで引ける意味不明な人。それが群論!
なんでー!数学と日本語は全くの別物でしょー!
じゃあこれ計算してよ。
12ab÷3a
>>2405
ソースは群論の具体例の構成に過ぎない。具体例が構成出来ないようですな。
「6÷2(1+2)」という割算が定義されない場合だってある。
ちなみに、サッケリの公理ってご存知? 内容的には中学でする初等幾何に比較的近い。
>>2405
一応いっておくが、ここに書き込んだのは、>>2386のような群論を全く知らない人間に、
私が愛する厳密な数学の考え方(群論による考え方)を否定されて、怒りをぶちまけたくなったからだ。
もちろん4b
9と答える人はどう答えるのかね。
答え方の違いや途中式をしっかり見せて欲しいもんです。
※2403さんはいくつになるのかな
ですよねー!
だから説明不足とかいう人の気がしれないです。
(分は分数の形で書くということ。分かると思うけど念のため)
中学校一年の教科書では÷ではなく分数の形で載ってる
分数だと6÷2(1+2)は後者の2(1+2)分の~になる。決して前者にはならない。
A÷BC=BC分のAだから。
別に÷は中学では当たり前の様に用いられてるけど?
間違いやすい書き方はするなって言うけど、計算問題なんだから当たり前。
勝手に間違って問題が紛らわしいとか自分の頭の悪さを棚に上げて文句言うのはどうかと。
÷って使っちゃいけないの?そうじゃないでしょ。
根拠示して欲しい。
分配法則の表記と一緒の場合、÷は分数の形で教科書には載ってる。
分配法則の表記と一緒でない場合÷は使われてる。
これなら分母と分子の数明白。自分は教科書に従う。
あと当たり前とか頭の悪さとか文句言うとか主観でしょ?
それ証明できる?
あと分配法則をちゃんと分かってる?
(2A+6)÷2=A+3
これも分配法則だよ。こんな問題はいくらでも転がってる
2分の1(2A+6)と言う分配法則ね(1÷2(2A+6)だと今回と同じ形になっちゃうでしょ) _ (1+2)
ただそういうことを言ってるのではないよ。教科書には6÷2(1+2)という表記ではなく 2 であったりとか
2
_(1+2)の形で表記されてるということ。(1+2)×2分の6や(1+2)×6÷2の形の表記もある。
6
言い換えれば教科書には6÷2(1+2)の形の表記はないということ。6分の2の場合も同様。
教科書のように表記すればこんなに論争が続くことはなかったと思わないかい?
数式を、×÷を使って表せ<ーー>×÷を使わずに文字式の形で表せ
なんて問題はよくある。
当然両者を混ぜることも可能。
正しい数式であれば×÷を使おうが省略しようが異なる答えになるわけもない。
改めてこのタイプの問題がいかに正答率が低いか再確認できたわけ。
9だ!1も9もある!と答える人は
6÷2A=3A 6÷2√3=3√3等を認めなければいけないわけだ。
そんな人間とまともに数学の話なんかできるわけない。
ちなみに()は一つの文字に置き換え可能。まさかこのルールも知らないわけではないと思うが。
あたりが正しい。
あと※2417は※2389?
申し訳ないが6÷2a=3aって言ってるようじゃ論外
自分の考えと現実のデータが一致しているとは限らないの分かってる?
自分がそう感じたから相手もそう感じるとは限らないの分かってる?
なぜ?こういうことを言ってるのか考えてみて欲しい
全くの同感です!
そうなんだよね。9の考え方は6÷2a=3aだし、そもそもそんな解釈の仕方は無いんだよ。
あるならそれを出せばいいだけのこと。
是非知りたいもんだ。
ほんと同じ考えですね!!
出会えてよかったです!!笑
でも実際a÷bcだと1のようになるのは確かなんだが
確かに
何でだろう?
うーん。わからんw
ただ、2と()の間に×を入れたら9になった・・・
これが違うなら関数電卓作り直してくれないと・・・
×いれると9になるのも同じ
こちらも関数電卓が1だから1が正解といいたいもんだ。
ちなみにグーグル電卓は他にもある計算ミスがあるようだから。
299999999999999-299999999999998=1は普通に出てくるのに
399999999999999-399999999999998=0
とでてくるらしいよ
ちなみにこれ以降
499999999999999-499999999999998=0
て出てくるらしい
今は修正されてるみたいだけど
つまりグーグル電卓もミスするのさ
そうなんですか!知りませんでしたっ!
8÷2√4=8
正しくは2
グーグルがとか言ってるバカはさすがにもういないだろ
2(1+2)でひとつの数字としてとらえるんじゃなかったっけ?
6÷2x=yみたいに
Google計算機で2(1+2)だけだと答え6ってでたけど、丸ごと式を入れると9になるという
数学の教師何人かに聞いたらどちらの答えが多いのかが気になるw
だから、解釈の違い。
6÷2(1+2)=6÷2×(1+2)っていう解釈がな。間違ってるとは思うが。
だったらそういう奴は6÷2a=3aじゃなきゃいけない。
6÷2√3=3√3じゃなきゃいけない。この答えを9とするのはそういうことだ。
9の解釈ってバカが自分の考え書き込んでるにすぎないからな。
男性1人と女性2で構成されている
家族が2組あります。
さて?林檎は一人!何個づつ貰えますか?
1個ですよね!
それを!表した数式です。
6÷2(1+2)=
1の解釈はわかるけど9の解釈ってA÷BC=AC÷Bだよね?そんなのどこにあるの?
正しくは1か式が間違いのどっちか
9はない
まあ、6÷3Aとか6÷3√2とか考えれば簡単。
数学に慣れていれば、自然と1という答えが出るはずなんだが。
あと7はもっとありえない。中学校から勉強やり直したほうがいい。マジで。まあ、ネタ、もしくは、9厨に対しての指摘だよな?w
3÷3a=
3÷3×a=1×a
=a
になるとでも思ってるんだろうか?
そうそう。まったくそうだ。
9派はバカだね。
a÷bc=bc分のa に a=6,b=2,c=1+2 を代入
6÷2(1+2)=2(1+2)分の6
6÷2(1+2)=6分の6
6÷2(1+2)=1
よって、「ある数」に「式」を代入した形だと理解すれば自然である。
ちなみに、CASIOの電卓でやってみたら答えは9になったし、ぼくも9やと思うけど。
1って答えでるのは、中学生レベル以上じゃなくて、中学生レベル以下の人じゃないかと。
6÷2(a+b)として、置き換えて見ろよ。
どう考えたって、3(a+b)になるでしょ?
そしたら、ここではa=1,b=2だから、自然と答えは9になる。
>「÷」じゃなくて、分数を使うはず。
の結果、あなたの考えでは、a÷bc がどういう形になるのか説明していただけませんか?
まず、 a÷bc=bc分のa というのが中学校の教育で教えられている事。まずはこれが大前提。
A÷BC=BC分のA に あなたの指示通り A=6,B=2,C=a+b を代入する
6÷2(a+b)=2(a+b)分の6
6÷2(a+b)=(a+b)分の3 (6と2を約分して3と1に)
6÷2(a+b)=(1+2)分の3 (a=1,b=2 を代入)
6÷2(a+b)=3分の3
6÷2(a+b)=1
まず、 A÷BC=BC分のA というのが中学校の教育で教えられている事。まずはこれが大前提。
A÷BC=BC分のA に あなたの指示通り A=6,B=2,C=a+b を代入する
6÷2(a+b)=2(a+b)分の6
6÷2(a+b)=(a+b)分の3 (6と2を約分して3と1に)
6÷2(1+2)=(1+2)分の3 (a=1,b=2 を代入)
6÷2(1+2)=3分の3
6÷2(1+2)=1
あなたは3a÷3a=a^2派なのですね・・・
はぁ・・・。
a=6 b=2 c=(1+2)
6÷2(1+2)=6÷(2+4)=1
a÷b×c
a=6 b=2 c=(1+2)
6÷2×(1+2)=6×(3)÷2=9
”a÷bc”と”a÷b×c”では結果が違う
”6÷2(1+2)=”は”a÷b×c”ではなく、”a÷bc”です
よって、答えは”1”
恥ずかしい発言ですね(^-^;
あなたこそきちんと、義務教育受けてないのでは?
私は9だと思いますし、1にはならない(かけ算と割り算は優先順位は同じです。)と思います。
1になる人は 6÷{2(1+2)}と勘違いしているのではないですか?
あと、6-2(1+2) ならば、先に2(1+2)を計算しますが、足し算や引き算と勘違いしているのでは?
中学校の教科書では A÷B×C=B分のAC、A÷BC=BC分のA と学ぶはずなんですけど、そこから考えるとどうしても1にしかならないんですよ。
A÷BC=BC分のA にA=6,B=2,C=1+2を代入
6÷2(1+2)=2(1+2)分の6
6÷2(1+2)=(1+2)分の3
6÷2(1+2)=3分の3
6÷2(1+2)=1
ゆえに、6÷2(1+2)=6÷{2(1+2)} と解釈するのが自然なんです。
”2(1+2)”と”2×(1+2)”は違います
3÷3a=a が間違いなのはわかりますか?
あなたのほうがどうやら義務教育を受けてないようです^^
>”2(1+2)”と”2×(1+2)”は違います
それは間違っています。
2(1+2)=2×(1+2) です。
6÷2(1+2)≠6÷2×(1+2) と説明しないと誤解を招きます。
”2(1+2)”は一つの項
計算結果が同じでも、表記の仕方で意味が違います
"2ab"は一つの項であって”2×a×b”ではありません
また、6÷2(1+2)もまとめて単項式です。
計算順位が解りにくいけど、6÷2(1+2)=6÷{2×(1+2)}というふうに解釈しましょうねって話です。
数学に“自然と”解釈なんて通用するって本当に思ってますか? 式にかかれた通りに“正確に”解釈しないといけないんです。
数学っていうのは、規則に厳密に従った世界なんです。 しかし、これはあなたたち小学生(レベル)にとっては難しく理解しがたいことでしょうが。
>式にかかれた通りに“正確に”解釈しないといけないんです。
>規則に厳密に従った世界なんです。
まったくおっしゃるとおりだと思います。すばらしい。
なんの反論の余地もありません。
なので、6÷2(1+2)=6÷{2(1+2)}=1
です。
なので、それぞれに A=6,B=2,C=1+2 を代入して、
6÷2×(1+2)=2分の6(1+2)
6÷2×(1+2)=2分の18
6÷2×(1+2)=9
6÷2(1+2)=2(1+2)分の6
6÷2(1+2)=6分の6
6÷2(1+2)=1
とりあえず9になる途中式を含めた過程を教えてください
あと6÷2aの答えもお願いします
6×2(1+2)=1
6×2×(1+2)=9
問題自体の表記が間違ってるけどあえて答えるなら1
ちなみにエクセルやグーグルは2(1+2)=2×(1+2)と勝手に解釈してしまうため、答えは9になってしまう。一方関数電卓は、2(1+2)をひとつの項として計算しているため答えは1になる。
この問題の表記通りの計算法なら1が正解である。
理解不能、計算も間違い。
間違った式から答えは出ない。式が間違ってるとしたら6÷2(1+2)≠1
式に誤りがあるなら6÷2(1+2)=1とは決して書けない。
その前に最低でも直後に訂正コメ入れるなり何なりしろよ
a^2=b^2+c^2-2bccosA
を
cosA=
の形に直した公式あるでしょ。
これといってること同じじゃん。わかるかな?
でも、教科書とかにのってるcosA=の形は1派の考え方。
つまり、9派は数学的に論外。
僕は関数電卓に従うよぉ
まあ1、9と答える以上式は正しくなければならない。
式が間違いとする主張は説明不足というかソースが無い。
一般に曖昧な解釈が可能な数式は避けることが推奨されており、可能ならスラッシュではなく分数の形で記述すべきであり、そうでなくとも括弧を使って曖昧な解釈ができない形にすべきである。
だって。曖昧な式なのに、かっこやスラッシュを使わないのは問題として如何なものかと
悪いが9は誤解っていうのが目的の問題だぞ?
6*0.5*3=9
なので、それぞれに A=6,B=2,C=1+2 を代入して、
6÷2×(1+2)=2分の6(1+2)
6÷2×(1+2)=2分の18
6÷2×(1+2)=9
6÷2(1+2)=2(1+2)分の6
6÷2(1+2)=6分の6
6÷2(1+2)=1
フィールズ賞受賞した森 重文いわく「演算子の優先順位通り普通にに左から計算しろ」だそうです
2(1+2)とも2×(1+2)とも読み取れるからな、項の数が変わる
個人的に2(1+2)は単項式の書き方っぽいだから1の方が好き
弘法も筆をあやまったってことか。
答えは1
前者は只の6、後者は2×3
中学校で×は省略していいって習ってるだろうけど何でもかんでも×を省略していい訳じゃない。
×を省略するには理由があります。
6÷2√3は6÷2を先に計算するの?
そう、それなんよ。
だから俺も絶対1だと思うし、答なしとか問題悪いとか論外だと思う。
現在では答えは1だと結論はでています
この記事は間違ったままのサイトからの転載であり
直ちに修正されるべきです
9が正解だというサイトは多いですが間違って拡散されただけです
9だと言う人はもっと調べてみて下さい
先進国でこれは恥ずかしいことです
3a÷3a=a^2って答えるのと同じでしょ?
なので、それぞれに A=6,B=2,C=1+2 を代入して、
6÷2×(1+2)=2分の6(1+2)
6÷2×(1+2)=2分の18
6÷2×(1+2)=9
6÷2(1+2)=2(1+2)分の6
6÷2(1+2)=6分の6
6÷2(1+2)=1 よって、6÷2(1+2)=1 が正解
9でしょ。
1の人の意味がわからない
6÷2(1+2)でしょ?
=3(1+2)→3×1=3 3×2=6
=3+6
=9
A,9
ーーーー
僕は9になりました
6÷2(1+2)
=3(3)
=9になりました
僕の考えの1は、
3(3)になったあとに6の後ろについてる÷を使って3÷3にしたんですか?
逆に1の仕方を教えてください
Xの省略はカッコ内で省略されているものです。
これは数式が増えて間違いが起こるのを防ぐために省略を許している訳ですからすべての数字、記号間に省略を可能としている物ではありません。
同類項はカッコで括れと言う言葉ご存知だと思いますが・・・
どうして1になるかわからない人はこれで理解できると思います。
出題者を含め解が9と答えている人は省略している部分を勘違いしていると思います。
そもそも、2X(1+2)と2(1+2)とでは意味が違います。
9だろ?
9だよ?
=6÷(2+4)
=6÷6
=1
いやいや分配法則使うのなら4もかけないといけないと思う
違うって()の計算を先にしないといけないって
同じですよ
()はⅹやyと同じ文字として考えるんですよ?
現役の中学生が言うんだから本当だよ
()をⅹと考えると
6÷2×xでx₌3だから代入法で
6÷2×3で左から順に計算していくと9だから
答えは9だと思います
なので、それぞれに A=6,B=2,C=1+2 を代入して、
6÷2×(1+2)=2分の6(1+2)
6÷2×(1+2)=2分の18
6÷2×(1+2)=9
6÷2(1+2)=2(1+2)分の6
6÷2(1+2)=6分の6
6÷2(1+2)=1 よって、6÷2(1+2)=1 が正解
(1+2)をⅩと考えます
そうすると6÷2Ⅹになりますよね?
Ⅹは3ですよね?
代入すると6÷2×3になります
もちろん左から計算すると9になります
なので答えは9です
X=1+2であれば、Xは当然3ですが、あなたの場合、次の行で飛躍しています。
X=3だからといって、6÷2Ⅹ=6÷2×3にはなりません。
中学校の教科書では、A÷B×C=B分のAC、A÷BC=BC分のA、というふうに区別して教えています。
そこに論点を絞ってもういちどよく考えてみてください。
6÷2Ⅹ において、x=3ならば
→ 6÷(2×3)=1
僕も昔疑問に思っていたのですが
Ⅹと()は同じだと言われたからそう考えたのですがやっぱり違いますかね
なぜ2×3に()をつけるんですか?
そこがわかりません
説明していただけると嬉しいんですが
=6÷2(3)
=3(3)
=3×3
=9
なぜ()から×に変わったかというともともとは結合法則で
(Ⅹ+y)×z=z(Ⅹ+y)だから今回はそれを逆にしたからです
これは中学校で習います(たしか一学期)
※2527 ※2526
まず、書店で中学校数学の教科書か或いは参考書を確認してください。
全てではないと思われますが、ほとんどのものに下記の説明が書かれています。
A÷B×C=B分のAC、A÷BC=BC分のA
※2525さんのいうように、()はXと同じように考えますので、例えば、C=()ならば
A÷B×()=B分のA()、A÷B()=B()分のA となります。
また、上記二つの方程式のそれぞれのA、B、()に問題の数値を代入してみましょう。
A=6 B=2 ()=1+2 です。 ()=3でも構いません。
6÷2×(3)=2分の6(3)、6÷2(3)=2(3)分の6 です。
それぞの方程式は右辺の分数と左辺の式が等式で結ばれなければなりませんので、
これで明確な答えが導けたと言えます。ご確認を
二つの方程式はそえぞれ以下のとおりとなりますので、
[1] 6÷2×(3)=2分の6(3)
[2] 6÷2(3)=2(3)分の6
問題の答えが9になるためには、[1]の形でなければならなく、
1になるためには[2]の形でなければならない事がわかります。
ここから導ける一つの帰結として、6÷2(3) のように、()の外についた2と()の結合関係は、
6÷{2×(3)}と考えるのが自然であるといえるわけです。
よって、6÷2(1+2)=1 が正しいといえます。
①の補則
「下記の説明」とは
「A÷B×C=B分のAC、A÷BC=BC分のA」の事です。
BCっていうのはB×Ⅽだと思います
それは文字式と同じで、たとえば7aだとすると7×aと同じだから
実際はA÷B×Ⅽと同じだと思います
補足ですが
②と③も同じです
すみません途中式をお願いします
答えが1と出ても9と出てもあってると思います
なぜかっていうと根本的に考え方が違うんですよ
1の人は数学的
9の人は算数的だと思います
なのでどちらも正解だと私は思います
※2535 ①~⑤までの全てをじっくり読んでみてください
※2536 数学も算数も同じです、矛盾しないからこそ数学が成り立っているのを理解してください
※2537 現代の常識の範囲内では使う事のない表現である という意味において同意です
数学と算数は違います
それではなぜ小学校の時は算数で中学校からは数学なんですか?
それにまず元から違います
もし同じだったらなぜ数学か算数どちらかに統一しないんですか?
逆におたずねして恐縮ですが、数学と算数の矛盾点をお示しください。
まず自分が知っているなかでは3つあります
①算数は『計算の正確性』が求められるのに対し数学では『論理の正確性』が求められるということです
②数学は算数の延長戦上にはないので勉強の仕方が違う
③数学は、算数のように丸暗記するのではなく『なぜそうなのか』を理解する
以上が自分が知っている違いです
①③については、そこには計算結果の矛盾は生じません。
②はなにをおっしゃっているのかよくわからないです。
が、いずれも数学と算数の矛盾点を指摘されているわけではなく、
数学と算数がまったくの別物だという説明にはなりません。
はあそうですか確かにわかりにくいですね
だけどこれだけは言っておきます
最初は9って言っていましたが答えはまだわかりません
俺にはそれを正しく証明できませんがいずれ答えがわかることでしょう🎵
諦めないで頑張ってね!
あ、これで、2545目だ!
ん?意味が分からないんだけど?ww
なので、それぞれに A=6,B=2,C=1+2 を代入して、
6÷2×(1+2)=2分の6(1+2)
6÷2×(1+2)=2分の18
6÷2×(1+2)=9
6÷2(1+2)=2(1+2)分の6
6÷2(1+2)=6分の6
6÷2(1+2)=1 よって、6÷2(1+2)=1 が正解
1じゃないと思うんだけどそれは俺だけかな?
でもこれは問題が悪い
しかもみんなは答えを求めているだけだからダメなんだよ
まずこの問題を作った人の意図を考えなきゃ
まあそう考えても俺にはわからないけどね
つまり言いたいことは人間の言葉は役に立たない
※2547に対する明確な間違いを指摘できたら信じてあげる
じゃないと1だとしか考えない
別に間違いがあるとは言っていない
自分が1じゃないっと思っただけで明確な間違いを指摘をする必要はない
ただあるとしたら計算の順序とかなんじゃないん?
※2547の記事を指して"1じゃないと思う"と書いているから、
1だと明示している※2547に対して反論してみてと言っているのです。
それで1じゃないと納得できる説明ができるなら、
あなたの意見に賛同すると言っているのです。
説明ができないのなら”1じゃないと思う”というのは、
あなたがぼやっと思っているだけの事で、意見にもなっていないんですよ。
うん、だからあなたがいちいちその事に対して意見する理由がないんですよ
ぼやっと思っているだけとわかっているのならわざわざ意見しなくていいんじゃないんですか?
そのあとの文をちゃんと見ましたか?大事なのは、答えじゃないんですよ。
じゃあ、最初から※2547に対してコメントしなきゃよかったね!
ごめんね!
俺もそう思ったところだよ!
仲直りっ!
うん!
2と()の間に×が無いんじゃなくて何故かxとかyとか使わない式が()の中に存在してると考える
9にするためには
6÷2と(2+3)の間に分かりやすく空白を作るとかしないと。。。
二次方程式の解は2つあるぜ?www