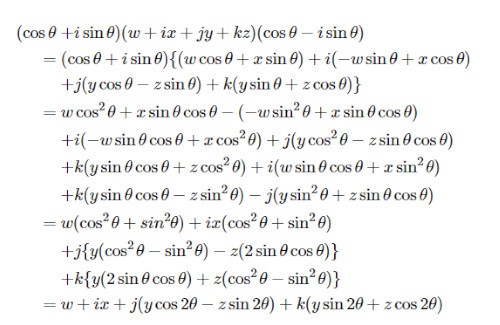
セガさん、社内勉強会用の数学資料を無料公開
サインコサインタンジェント、虚数i…いつ使うんだと思ったあなた。実は数学は、ゲーム業界を根から支える重要な役割を担っているんです。
— セガ公式アカウント🦔 (@SEGA_OFFICIAL) June 15, 2021
今日は、セガ社内勉強会用の数学資料150頁超(!)を無料公開。#セガ技術ブログ クォータニオンとは？基礎線形代数講座 #segatechblog https://t.co/OEHDwlJ9Vz pic.twitter.com/eBUG2YJwH1
クォータニオンとは何ぞや？：基礎線形代数講座
数学の勉強会
弊社では昨年、有志による隔週での数学の勉強会を行いました。ご多分に漏れず、コロナ禍の影響で会議室に集合しての勉強会は中断、再開の目処も立たず諸々の事情により残念ながら中止となり、用意した資料の配布および各自の自学ということになりました。
勉強会の内容は、高校数学の超駆け足での復習から始めて、主に大学初年度で学ぶ線形代数の基礎の学び直し 、および応用としての３次元回転の表現の基礎の理解といった感じです。
「線形代数」とは、微積分と並び理工系の科学・技術の諸分野で基礎中の基礎として用いられる数学の分野で、ゲームでは主に3DCGの技術的基礎として応用されています。昨今のAIブームでも一時期話題になりました。 タイトルにある「クォータニオン」とは、日本語では「四元数」と訳され、ゲームではキャラや背景などを３次元回転させるときに応用されるもので、勉強会の中では最後に出てくるラスボスであり少し難しい数学の概念です。
勉強会の趣旨は、この「クォータニオン」を数学的にきちんと理解することを えさ ゴールとして、そのために（実際はそれだけでなくさまざまな技術の基礎となっている）「線形代数」の基礎をきちんと学び直そうということでした。
なぜ数学？
ゲーム開発においても分業化・専業化の流れは著しく、ゲームアプリケーション（みなさんに遊んで頂いているゲームそのもの）を開発する際、いわゆるゲームエンジンや各種ライブラリを用いるのが当たり前になっています。これらエンジンやライブラリは、ゲーム開発者にさまざまな機能を提供し効率よく開発できるようにすることが役割であり、極端な話、三角関数を全く知らなくても３Dゲームを作れる時代になっています。 しかしながら例えばゲーム固有の表現のためにシェーダー（画面を描画する機能）をカスタマイズしたい場合や、当然のことながらエンジンやライブラリそのものの開発者は、ある程度のさまざまな数学の知識が必要となります。技術的に高度なことをしようと思うとなおさら深い理解が必要です。
このように数学や物理学は、ゲーム業界のみならず理工系のさまざまな分野で、科学者・技術者を根元から支える基礎となり重要な武器となっています。
以下略
ゲームでは、膝や肩など、3次元の回転を4次元を使って表現するクォータニオン計算を使用することが多いため、ゲーム開発者はよく使う数学なのですが、仕組み理解のため社内勉強会が開かれたのでした。
— セガ公式アカウント🦔 (@SEGA_OFFICIAL) June 15, 2021
「大人の学び直し」してみたい方、ぜひ→https://t.co/OEHDwlJ9Vz #segatechblog #セガ技術ブログ pic.twitter.com/CHb9sqE3pi
エンジニアのみなさん、ゲーム開発に興味のあるみなさん。セガでは共に技術力を高め合い研鑽していていける方を募集しています。 活発な技術知見交流やバックヤード部門も加わるゲームジャムイベントなども。興味がある方は下記サイトにアクセスしてみてくださいね。 https://t.co/qADRDRNpMG
— セガ公式アカウント🦔 (@SEGA_OFFICIAL) June 15, 2021
この記事への反応
・自分は何が何だか解りません（泣）
・こういうツイートを10年前ぐらいに見たかった!
ゲームが好きな学生とか作ってみたい人とかには、頑張って数学を勉強しようと思える材料。
・ゲームを作るためには数学を勉強しなければならないですね。
・ゲームばっかしてるとアホになる！って親御さんに言われた子は、これ、ゲームの裏側っていって見せてやればだまりますね。表しか触ってないだろって言われたらあれですが
・ゲーム開発＝ほぼプログラミング＝ガッツリ数学は関係してくるってことですものね…。
皆さんさも当然のように『応用処理技術者』以上の資格持ってそうで…。
・三角関数を使う機会は多々あれど、虚数を使ったことは今のところないな。
ゲーム業界では使うのか。面白いな。
・電気の交流回路の計算などにも複素数が使われていますが、虚数の概念が現代文明を支える大事な役割を果たしていることを、高校の数学の授業で教えて上げてほしいなと思います。
・ゲーム制作で使われることはよく知られたことではあるし、実装するだけなら裏側まで知らなくても多くは何とかなるという話も聞くけど、それでもセガさんが数学って使うよと言ってくれると若い人達の勉強モチベーションに繋がるでしょうね。素晴らしいです。
・セガさん、ぜひ中学数学の範囲でもゲーム業界への貢献度を語っていただきたいです。
・セガの社内勉強会の資料を無料公開ってすごい…3DCGの技術的基礎を学べるチャンス
なるほどな・・・見ても全然わからねぇや
やっぱり現場より上が間抜けだからサクラ大戦とかPSOとか56しまくってるんです？
学生の時に教わっているから社会人になってからも着いていけるんだぞ。これが社会人になってから一から勉強して覚えろって絶対無理だぜ
何となくそれっぽいこと言ってみただけだが？
日本が没落したのも、数学ができない人間が政府中枢に蔓延っているから
場の空気や人間関係に意思決定が左右される風土病も、数学力の不足からくる論理的、演繹的思考の欠如によるものだ
いらねぇだろ これ
これがソニーとかなら説得力あんだけど
そうですか
え、鳩山由紀夫は東京大学工学部計数工学科卒業だよ？？？結果はどうだったの？？？教えて？？？
もちろん売れてるんだよね？
こんなん勉強しないでアンリアルエンジンでいいわ
プログラミングより面白いことなんて、この世にひとつもないぞ
NGSがあの有様だったのが悪い
終わってんな
デザイナーも仕様理解が重要になるから学校の勉強はしておいた方がいいぞ。
虚数は全く使わないしもう忘れたけどな
わかります
スッと頭に入ってこない
E3にも参加できない泡沫メーカーか
スポーツ観戦だの音楽だのゲームだの同じだろそれらに何の役に立つか聞くのか？
数学も古文も漢文も全部楽しいからやるんだよハゲ。
数学より学ぶべきことがあるのでは？
.|-O-O-ヽ |ええと、みっつ の次は・・・
(. : )'e'( : . 9) ・・・たくさん！
複素数分からなけりゃ極座標扱えないからな。
自分と相性のよい講師とか自分で選び放題だし。
ソウルリバース頓挫
何で稼ぐの
ありていに言えば「数で割り切れないことがある」って話になるんだけど、
そもそも、会社の会計ひとつとっても、数学の公式がピッタリ当てはまる局面なんて珍しい方。
だから知っておくことは大事だけど、数学的演繹のみでは現実への対処ができない。
アベノミクスなんぞ数学の基本から言えば、破滅への時計早めた愚策だが、
多数派占めた政党と政府がゴーサイン出してるのに、数学的におかしいと跳ね返せると思うのか?
ゴキちゃん・・・
AAを弄くる暇でもうちょっと勉強しようね
ノーマンズスカイとかも数学の塊みたいなもんだろうしな
うんうん、わかったから少しは家の外に出ろよ。
セガの採用基準が間違ってる証拠でしょうが
内積外積も使う
微分積分も使う
行列も使う
どう使っているのかを教育現場に伝えないと何のための勉強なん？ってなるのは当然なのに覚えさせる事しかしねぇもんな
じゃあ君はやらないで好きにどうぞと放って於いて言わせておいたらいいのに
自分は上手いと勘違いしたガキリーマンを雇う2ちゃんねらー開発
案の定ソウルリバースは頓挫
先ずそこが欠けてる
明確な目標もないのに道具ばかりあっても何か生まれるようなものでもないぞ
そもそも勉強って何かのためにすんの？ただ突き詰めるのが楽しいからやるんちゃうの
結果的に役に立ったら素晴らしいだけで
行列、複素数(四元数)
最低、これできないと3Dはちょっと
そのエンジンがどうやって出来てると思ってんだよ
「アインシュタインの相対性理論がなかったら、スマホの発明はなかった」
とも言われてるな。
ゲームばっかしてるアホにこれ見せても99％が理解できないから親が正しい
それに真正面から挑むより解決するための自動作成エンジンなり作ったほうがええやん
問題はそいつにセンスがあるかどうかってことだけ
算数ができないと買い物もできなくなるから必要性はガキでも分かる
数学が何の役に立つかも教えてやれるべきではある
大昔は暇人が趣味でやっていた学問だった位だし、使い道が無ければ無意味に思えるものだ
自前で作ろうとしてるとかなの?
学歴で採用してるからこんななんだろうな
「高学歴社員が組織を滅ぼす」ってやつだ
保身に長けた彼らは絶対に責任を取らないよう立ち回りリストラから生き延びる
ケチつけてる奴って、頭の悪い奴が殆どだろうなｗ 拒否反応が痛々しいｗ
どんなに優れたビジョンがあっても、それを具現化するテクニックがないと、ただの「絵に描いた餅」だ。
いや、餅の絵を描く事すらできない。
マジで無駄な時間だった
A. いわゆる「4要素ベクトル」が超多用されとるけえ
3要素ベクトルとかもあるんだけど、基本的にベクトルは4要素なんで
そうすっと、行列での計算が簡単だから
その曲がり方を数式で言う
そのゲームエンジンも、「誰かが作ってる」んだよ。
逆に言えば数式以外に表しようないしな
さすがに高校レベルは出来ないほうがはずかしいだろ知るかと逆ギレしていいのは大学の範囲だけ
長嶋茂雄も数学ができればバットの振り方を数式で教えてやれたのにな
取り敢えず、理系できる奴はサイコー、かっこいいよって子供は小さい頃から洗脳教育するのが吉なんだよな
あとゲームの面白さはゲームを動かすことも重要だけど、やっぱ脚本だよな！
もしくはゲーム自体の構成力！
四則計算・分配法則だけ知ってりゃ生きてけるんだよっ！！
何やるにしても数学は理解しておいて損はないと思うが
そのゲームエンジンでもどう回転させるかは指定しないといけないわけで
これ英語だよね？
いや、教師が社会に出た事が無いから何に使うか単純に知らないんだ
まぁなんかやれる具体例の一つとして上げただけだろ、何かにつけて計算する必要はあるし
簡単な三角関数、微積、虚数
この程度がわからないやつが何ができるんだよ
大体の学問で使うだろ
なるほど…
今のセガのこの有様は技術屋に渡す設計図作ってる側が無能揃いなせいなんですかね？
勝手に分解すんなよ。
自然のままにしておけよ。
コスパ最強だし一生難関ボスみたいなの出てくるし達成感あるし自分の成長すげぇ実感できるし
数学(数理)の博士号持ってないといけねえ！ってのは、そこまで多くない
ガチレースゲー、ガチ飛行機ゲー、AI、それらいわゆるシミュレーション分野ならまだしも
学校で講義聞いてりゃ分かる、くらいだ
ただしプログラマーは数学好きが多いんで、勝手に博士レベルが集まってくるものだ
高卒ニートかFラン文系の非正規くらいだろう
i✕i＝－1
i✕i✕i＝－i
i✕i✕i✕i＝1
i✕i✕i✕i✕i＝i
これを利用すれば、虚数軸と実数軸を行き来出来るんだよ
ご縁がなかったということでw
３Dモデル動かすのにこんな知識は要らんぞ
エンジン自体を作るなら必要なんだろうが
なに使うんだよ
営業で使うのこれｗ
それで作ったサクラ革命はどうでしたか？
「量」の変遷、「状態」の変遷、「空間」の変遷の3つだけ
量を取り扱うのは例えば素数、複素数、四元数
状態の変化を取り扱うのは、例えば微積分、力学、ベクトル
空間を取り扱うのは、ここでもある線形代数や、幾何学
たいしたこたぁない
理系はもっと楽しい自分の研究があるわけで
近代文明の発展に必要な分野は大体網羅してる
化学の実験系の分野だと虚数まで使うことはなかったな。
分析機器の開発とかだったら使のかもしれんけど。
説得力あったんだが
目的が欠落して手段だけ伝えられとしても身に付かん
サクラは許さんけど
コンセプトからして破綻してる
ツールや開発ソフトやOSなどコアな部分を作る人らに必要ってだけ。
それらのソフトを使っていわゆるコンテンツを作る側の大半のクリエーター達には必要ない。
多過ぎて効率悪いだけじゃね
量子力学やるような奴は虚数程度でつまずかんだろ。
自分用の営業資料やプレゼン資料作る時に統計学くらいは使った方がいいぞ。
高校レベルの数学でできるで。
自分で工夫しないお使い営業ならいらんやろうけど、
それがキミの考える営業ならそれでええんちゃうか。
クリエーターも普通の人らには入らんと思うが
一切使わないのは無いだろうけど高度な知識を必要としない仕事は山ほどある
i→正面を向く(何も起きない)
i✕i＝－1→左を向く
i✕i✕i＝－i→後ろを向く
i✕i✕i✕i＝1→右を向く
実際に使う数学（工学部）を大学で勉強してない教師しかいないから。
設計や開発では普通にやってることを、中学や高校の教師は知らないので、質問しても出てこないよ。
技術者は使うものだから
PCを触ったことの無いIT担当大臣がいた国を舐めるな
これできねえとマジで入口にも立てねえからな
行列だけは完璧に理解しておかんといけん
んで、行列が分かれば自然と線形代数も分かる
面白いゲーム作ってから言ってくれ
必要な時に必要な数学だけ使えば事足りるのに、数学全部やった方が役に立つ。の脳死はアホ。
そして大体の人は数学を多用することは無い。
国家成長の為の全体論としては必要だと思うけど、実の所はやりたい奴がやれば良いだけ。
ファミコンレベルのプログラムが出きる新卒は即採用レベルだろ
ファミコンレベルとバカにするなら自分で1から勉強してみると良い
案外バカに出来ないよ
希望退職者650人募ったら700人来たんだっけ？
プログラム授業とかやっても意味がないのよ
適性がないとできない、完全な選民思想・適性重視だから、
授業でやった程度ですら面白いと思えないやつはもうダメなのだ
いや、ビジョンが先だな、技能はその後だ、モチベーションが続かなければ技術も身に付かない
それはセガ見ればわかる
最悪ド下手クソでも努力すれば餅ぐらいは描けるんだよ
適正にあった進路に進むべきだよな
餅は餅屋に任せよう
担当違いに的外れなことを言ってやるなよ
交流理論で出てきます。
但し、電気理論においては「ｉ」というのは
「交流電流」を意味する記号として
リザーブされていることから
虚数は「Ｊ」で示します。
そういう適性を持ってる奴を探す為もあると思うぞ学校の授業は
つまり職業適正が、ない
うんちくじゃ面白いゲームは作れないぞ
数字を全く見ていない経営してるとしか思えないからなぁ
なんだあの万年赤字体質
馬鹿だから馬鹿みたいな事言ってるんだろうけど
新サクラ大戦のプロデューサーとディレクターは、ウィキペディアに書いてあるアイツらだよ。
新サクラ大戦の出来上がりを見て名越が予算を切り、その分をジャッジアイズや龍が如く7に振り分けたんだよ。
あの仕上がりでは妥当な判断だろ。
社員が有能でも経営者が有能とは限らない
そんな会社はゴロゴロあるよ
俺らの時代は高校でやらなかった記憶がある
行列と線形代数は切っても切れない固い絆で結ばれているので
その行列が大学からだったから、高校ではやっぱりやらなかったと思うな
ってことは、高校レベルの数学ではダメなのだから、プログラム授業はなおさら意味がない
建築、施工系も必須だし、あって困ることはないで。
そういうことだろ
ボトムアップじゃなくてトップダウンで出た技術覚えないと追いつけない業界なのに見事に技術的に置いて行かれてる理由がこれだろうな
経営者を見切れない無能の分際で有能気取りとかよくいるよね
原作レイポゥ
そのシステムでゲーム作っているところは特にそのへん理解してなさそうだけど
実際のところどうなんだろう？
っていうようなアホ理論
UnityやらUEをカスタムとか拡張無しで使ってるゲーム企業なんてまずないぞ
経営者に必要なのは数学じゃなくて会計の知識
グラフィックが綺麗なだけの単純なゲームしか求めてないんならいいだろうけどな
マジでちゃんと勉強して来て欲しい
これを理解できるやつがいなきゃゲーム作りは難しいってだけ
何をそんなに怒ってるやつらいるんだか
ちがわんだろ
セガオリジナルプロトコルとかあるんだってよw
その話聞いてセガへの派遣断ったもんw
外で役に立たないことを身につける暇はないw
ゲームエンジン作った人に感謝しろ
そんな古臭い無駄な勉強させるくらいならゲームエンジンのオペレート習熟度上げさせてどうぞ。
煩雑な情報ですごい感を出したいんだろうけど
現代のゲーム開発環境では座学で1から学ぶのは非効率的すぎる。初っ端からツールを触って何かを作らせるのが最適解
そんなんやってるからいつまでもセガなんだよ
それで出てきたのが新サクラなら怒りたくもなる
開発はセガじゃない。。。
大手はどこも開発してるでしょ
そのエンジン作ってるのもゲーム会社だけどな
セガだって自前のエンジン持ってんだから使ってんだよ
バカがにわか知識で長文披露するな
エンジンを作るなら別だが
文盲乙。
それはバーチャファイターが悪い
ゲーム会社のあたりまえを言ってるだけだし
そこは別に関係なくない
セガが嫌いで嫌いでしょうがないっては伝わるけど
ドラゴンエンジンってセガ作じゃないの？
セガが嫌いなんじゃなくて
ネットで見た話題を鵜呑みにしてるから駄目な面しか印象に残ってないし、他の面を知る気もない
自分は触ったことも無いゲームをこうして掲示板なんかでクソゲークソゲーとふれまわってる狂人だよ
PS2が成功したのは、ソニーのゲームエンジン『エモーション・エンジン』が傑作だったから。
ソフトウェアでソニーは勝ち、これがPSPの開発に繋がる。
ところがPS3ではチップ開発に失敗。
こう見ると、【任天堂】は一貫して、『チップ開発』が天才。
セガ制だね、他にヘッジホッグエンジンとかもある
開発は当然として、QA側もある程度は把握してないとダメ
ただの暇人の暇つぶしか
他に楽しいこと見つかるといいね
普通は使わないから高等教育であって、それを学んだという経歴を作るためにわざわざ試験を受けてまで入学したわけやん。学んだ知識の使い途は自分で考えるものであって、他人に用意してもらうものではないぞ笑
てかそんなもんお互い様ってだけの話
分業でやってんだから
理系ガ―、文系ガ―みたいな話に至る奴はただのアホ
プログラミングは数学が大事なんだが英語圏で作られてるから英語も分ると更に捗る
日本語圏プログラマーになかなか天才が現れないとされる由縁だな
役に立つときは役に立つ。
「論理的思考を磨く」とかいう文系の頓珍漢な意見は何なのだろう？
知ってたら開発に一々問い合わせんでも対処できる
車運転だけできるよりメンテナンスできるドライバーはいて困る事はない
そりゃそうだが、そんなこと言ったらなんだってそうだ
設計士だって現場の職人作業できたほうが確実にいい建物作れるが、できないやつが大半だから、細かいとこに気が回ってない建物がバンバン作られるわけで
↑この発言をした人は誰なんだ？
経済系でも使うし。数学力は収入に直結する
youtuberとか芸人やるんなら知らん
そのころまだ良い教科書になる本が無かったから凄く苦労した思い出
ただ高校時代ちゃんと数学理解してたかは如実に現れる...
普通のサラリーマンには運転免許のほうが重要性高いよ
類人猿に近い世界観なんだろうか
もっと役に立つ知識が他にもあるのに
既存の必修科目が時間割を占拠しているせいでそれを学べない。
時間と労力は有限だ。
今の中国人、学歴とんでもないぞ
エンジンの無かった時代でも開発に参加してた人が言うんならいいんだけど
ゲームエンジンから入ると、ゲームの処理と画面の演出の区別もつかない人が居たりするからな
「スプラトゥーンの解析完了」とか言っちゃったりして
学校全てに教習場の設備を用意するのは非効率なので専用に特化させた今の形が良いね
出来る人は教習を飛ばして試験だけで免許が取れる仕組みは真似して欲しい
3Dゲームは全部これ使ってんぞ
Unityとかのゲームエンジンを使ったゲーム程度の上位レイヤーでも使う
典型的な無能
数学使用する所ほど重要部署や業種、そこあぶれた者が何かに理由付けて数学不要論出すだけ
クソみたいな挙動のなんちゃって3Dゲームなら作れると思うけど
私達の暮らす社会は数学を使わない無能のほうがはるかに多いので
無能に合わせた内容にせよという話。これは数学不要論ではないのだ。
アウトプットがクソゲーなら折角の技術も無意味じゃん
文系資格なんて記憶でどうにかなるけど、数学は記憶だけじゃ解決できない
だから日本が中韓に電子分野ビジネス追い越されてる
無能上層部に合わせ技術者蔑ろにして冷遇するからな
本当は自社制作したいけどゲームエンジンを作れる数学的才幹は貴重なんだ
だからSEGAは出直し的に数学の夜学までしてるのに・・・アプリゲームに慣れてるとなぁ
ウチの会社、全社員ある程度のプログラムできるようにしろ、資格とれみたいな社員教育をするみたいだけど
「プログラムを覚えろ」って言われて覚えられるもんじゃないよな
俺は今はゲームと関係ないデザイナーだけど、子供のころ、家にあったベーマガのバックナンバーでゲーム自作するのを目標にして覚えた
数学はスポーツでいう筋トレのようなものだ
数学はおろか経営の基礎知識も無いアホだけど稼いでる訳だが。
プログラマー的には止まってしまうんよね
その仕組み作ったグーグルなんて数学博士号がｺﾞﾛｺﾞﾛいる
彼らも相応に稼いでいる、彼らの舵でyoutuber食わせてる事を忘れてはならない
論理の飛躍だ。数学が得意でも他が足りない技術者は昇進できない。
ほとんどのYouTuberは数学が出来る人より稼げてないよ
※271
YouTubeを見たり動画を投稿するのに数学は必要ないね
自分が「複雑な数学が要らない程度の社会で生活してる」からって
数学を活かせてる、必要としている人たちをバカにしてるのって、どんだけみっともない事をやってるか理解できないのかな・・・
有象無象の中に隠れた優秀な原石を育むために必要なのが教育なのであって
本当は無能には歴史も音楽も体育も学ばせる必要などなく蔑ろにして物事を進めたい
選別されてすでに無能しかいない状態なら全員ロボットのように単作業をこなすだけの洗脳がベストである
エンジニアじゃない人もいる大衆に発信して、自分の土俵のスキルをアピってくるのがきつい。
観念的だね
例えばユーザーが電化製品をうまく使うためには製品説明書が必要なのに
今はエンジニア用のマニュアルを渡しているのでそれを改めようという提案だ
要するに一部の融資で使ったハリボテ資料
被害妄想
スクエニに移った人も「セガでは」凄いと称えられてたけど、いざスクエニに移ったらクソゲー出して辞めたしな
「要らない程度」ってのは主観でしかない偏見だけどな
無能に必要なのは説明書ではない
何も解らなくてもボタンを押すだけで完結する便利な道具
困ったときは金を出せば解決する
ただただ経済を回すだけの存在であれば良い
セガ 「アホか、ゲーム開発に使うやろ」
セガ自体がオワコンになってんだな
ここまで落ちぶれるって相当だぞ
アルゴとAIの区別がついてなさそう
そもそもがどの業種でも売り上げなり何なりで統計触るなら結局数学知識無いとお話にならないのだ
「何かエクセルで『グラフ』って書いてある機能使っただけで何でこんな線かはわかんなーい！最小二乗法？なにそれ」
って言う奴はAI以前に役立たずで切られるのだ
奥義を極めてていいね
指先ひとつでダウン症さー
お前は学歴も職歴も何もないニートじゃんｗ
RPGの自称AI「お、新しい敵やな、ザラキ！ザラキ！ザラキ！」
開発者「ゼビウスには非常に簡単なAIが組み込まれています。」 → 今だとただのランク上昇システム
こんなだった記憶
当時としては頑張ってるんだろうけど
線形代数が使えなければゲーム云々以前に、そもそも３Dの画面表示が出せない。
クォータニオンはアニメーションやデータ圧縮で当たり前。エンジン使うからイランて？
エンジン使おうが数学ライブラリは利用するし、間違った演算をすれば正しい結果は出ない。
数式がわからない奴がどうやって数学ライブラリを使うんだい？ｗ
わからなければ、何が間違っているかも調べる事すらできないわけで。
専門職じゃねーわな。
経済・測量・建築・IT機材設計・暗号通信・コンピュータグラフィックスなど上げればきりがない。
世の中至るところで数学は使われてるし、
そんな事すら理解できないような奴はマックジョブ止まりだし納得だわ。
まともな奴は自分が使わなくても重要な学問である事ぐらいはわかってるよｗ
まあそんな奴は複利もわからず金利計算もできないので、リボ払い喜んでつかってそうで草草草
プログラムだけでも別れてるし大半の手間はグラフィックだよ
同じ質問をおばちゃん数学教師に聞いたら
受験のためやと吐き捨てられて
受験のためようの勉強の熱意しかもてんかったよ
という企画で、「ゲームを作れるようになろう、そのためにはこの知識が必要」と言ってるわけではない
エンジンつかうなら数学の知識なくてもゲーム作れるよ
いや、ゲーム開発とか興味ねえんだけど
全部高校数学の範囲だ、学歴とは。せめて大学レベルでいうならごもっともだが
なんとなくでもやっといてよかった
ベクトル空間と違って割り算があるから？
力学は物理やし、線形代数にベクトルが含まれてるんだから別々に書くのも意味わからんな
バカは喋んな
むしろ使わないゲームなんて無いのでは
求める数をｘにして一次関数にするのは便利
アレされて今でも精神ヤられてるのが周りにいるよ
虚数なんぞ使わん
使う時にでも覚えたらいい
虚数なんぞ使わん
使う時にでも覚えたらいい
やっぱあるのか。
鈴木さんも、中さんも、名越さんもあれだけ貢献したのにひどい扱いだよな。
正直、ゲームに関わるのは人生の浪費だと思うわ。若い人間を引きずり込むな。
まぁ働く直前まで知らないから高校生が知らなくても無理ないけど
教育の現場では、この分野を身につけるとこの業界の仕事に役に立つ、とかも教えたほうがいいと思う
それだけでモチベが上がる
なんの役に立つかわからないものを勉強してるときほど時間のムダを感じることはないからね
使う直前に勉強始めてるようならスタートダッシュに大失敗してるんだよなぁ
ゲームの開発を始めるまでに時間かかりすぎでしょ
だったらある程度知識があるやつを採用するわ
みんながみんな知らないわけじゃないからね
すげーな
お手本のような論点すり替えだ
とりあえずお前が勉強嫌いなことはわかった
この記事読んでこういうこと書いちゃうやつってホントアホだなぁって思うわ
数学だけじゃなくて国語も点数低そうだな
今ここが何言っても説得力ないよな
例えば肩関節なら
胴体から垂直に突き出した軸を中心に三次元で腕の角度を決めるけれど
歩くために腕を振り子状に振りたいなら
軸そのものを回転させたほうが簡単じゃろ
だから４つ目のパラメーターがあると便利という話じゃない 知らんけど
最低限の基本をやっているようなものだし
まあ使わなきゃすぐ忘れるけどやり直したときにすぐ覚えられるからな
麻生太郎みてるか？
10数年前にセガ社内でそんな事があったそうだが、今は無いと思う。
鈴木裕さんは興味が他に移ったのもあるし、年齢的に一線から引退だろ。
名越は心臓手術をしたのもある。
龍が如くスタジオの監督をして忙しいのに、更に重責を担わせて◯す気かよ。
中は自業自得だよ。
7次受け見たいな仕事斡旋ばっかやろうとするんだろうな
ゴキよ、これがクォータニオンだ！
とか言ってるやつに見せつけてやりたいわ。
お前もこれが分かるんか？と。
最近ヤクザーばっかりじゃん
おもしろいゲームを作ってくれよ…
だから和ゲーってつまんねーんだろうな
高校で古文教えてなかったら一から勉强する必要あって大変やろ
三角関数とか虚数を高校で教えるのだってまったく同じことやろ
必要になってから大人になって勉强するなんて実際はかなりハードル高いし無理やで
三角関数程度いつでも覚えられるだろ
デイライトワークスの数字に惑わされちゃったんだろうなあ
使えないと仕事にならないって程じゃないけど
義務教育の知識を使えるか使えないかは技術屋のスキルに直結する
ゲームばっかやっててもゲーム会社に入れないというのを早めに気付かせないとな
ありがとうセガ！
ゲーム会社で使いますは反論になってない
海外に行かず本も読まないなら英語も要らないし、物理化学歴史も生きる上で要らんしな
キミは中卒で働いてくれれば十分人の役に立つ